Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(F=3\sqrt{5}+\sqrt{30}-2\sqrt{15}-2\sqrt{10}-3\sqrt{5}-6\)
\(=\sqrt{30}-2\sqrt{15}-2\sqrt{10}-6\)

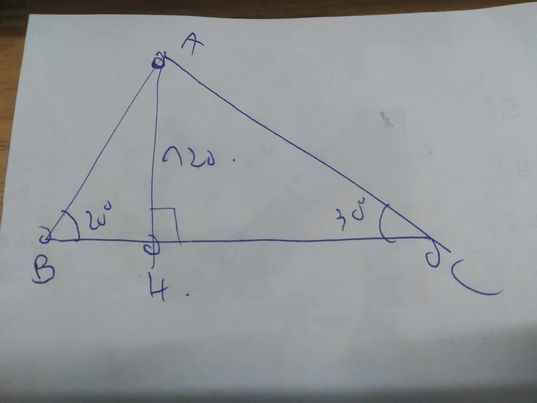
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát

Đặt tam giác ABC vuông tại A với B là đỉnh tháp
Áp dụng tslg trong tam giác ABC vuông tại A:
\(tanC=\dfrac{AB}{AC}\)
\(\Rightarrow tan30^0=\dfrac{26}{AC}\)
\(\Rightarrow AC=\dfrac{26}{tan30^0}=26\sqrt{3}\left(m\right)\)

Ta có :
∠ABC=90°−60°=30°,∠ACB=90°+30°=120°⇒∠CAB=180°−30°−120°=30°⇒∠ABC=∠CAB∠���=90°−60°=30°,∠���=90°+30°=120°⇒∠���=180°−30°−120°=30°⇒∠���=∠���
⇒ΔCAB⇒���� cân tại C⇒AC=BC=100m⇒��=��=100�
Ta có:h=AC.sin30°=100.12=50m

Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)