Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3/ (Bạn tự vẽ hình giùm. Vẽ hình dễ)
a/ \(\Delta ACE\)vuông và \(\Delta AKE\)vuông có: \(\widehat{CAE}=\widehat{EAK}\)(AE là đường phân giác của \(\Delta ABC\))
Cạnh huyền AE chung
=> \(\Delta ACE\)vuông = \(\Delta AKE\)vuông (cạnh huyền - góc nhọn) (đpcm)
b/ Ta có \(\Delta ACE\)= \(\Delta AKE\)(cm câu a) => AC = AK (hai cạnh tương ứng)
Gọi M là giao điểm của AE và CK.
\(\Delta ACM\)và \(\Delta AKM\)có: AC = AK (cmt)
\(\widehat{CAM}=\widehat{MAK}\)(AM là đường phân giác của \(\Delta ABC\))
Cạnh AM chung
=> \(\Delta ACM\)= \(\Delta AKM\)(c - g - c) => CM = KM (hai cạnh tương ứng) (1)
và\(\widehat{AMC}=\widehat{AMK}\)(hai góc tương ứng)
Mà \(\widehat{AMC}+\widehat{AMK}\)= 180o (kề bù)
=> 2\(\widehat{AMC}\)= 180o
=> \(\widehat{AMC}\)= 90o
=> AM \(\perp\)CK (2)
Từ (1) và (2) => AE là đường trung trực của CK (đpcm)

a) xét \(\Delta ABC\)CÓ
\(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=36+64=100\)
VÌ \(100=100\)
\(\Rightarrow BC^2=AB^2+AC^2\)
VẬY \(\Delta ABC\) VUÔNG TẠI A
trong tam giác ABC ta có :
AB2=62=36
AC2=82=64
BC2=102=100
ta thấy : 100=36+64 => BC2=AC2=AB2( định lý pytago đảo )
=> tam giác ABC vuông tại A
CHÚC BẠN HỌC TỐT !!!

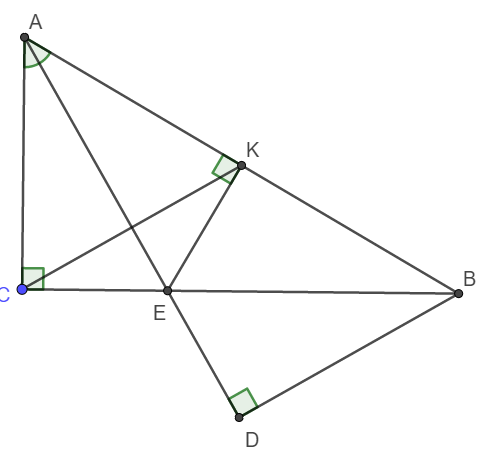
a) Xét tam giác vuông ACE và tam giác vuông AKE có:
Cạnh AE chung
\(\widehat{CAE}=\widehat{KAE}\) (gt)
\(\Rightarrow\Delta ACE=\Delta AKE\) (Cạnh huyền - góc nhọn)
b) Do \(\Delta ACE=\Delta AKE\) nên AC = AK hay tam giác ACK cân tại A.
Vậy thì phân giác AE cũng đồng thời là đường trung trực của CK.
c) Xét tam giác ABC vuông có góc \(\widehat{CAB}=60^o\Rightarrow\widehat{CBA}=30^o\)
Xét tam giác AEB có \(\widehat{EAB}=\widehat{ABE}\left(=30^o\right)\) nên AEB là tam giác cân tại E.
Vậy thì đường cao EK đồng thời là trung tuyến hay KA = KB.

1
B A H C M D
a) Xét \(\Delta\)ABC:AB2+AC2=9+16=25=BC2=>\(\Delta\)ABC vuông tại A
b) Xét \(\Delta\)ABH và\(\Delta\)DBH:
BAH=BDH=90
BH chung
AB=DB
=>\(\Delta\)ABH=\(\Delta\)DBH(cạnh huyền-cạnh góc vuông)=>ABH=DBH=>BH là tia phân giác góc ABC
c) Áp dụng Định lý sau:"trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền"cho tam giác vuông ABC, ta có:AM=1/2BC=CM
Suy ra \(\Delta\)AMC cân tại M
2.
C B A H
a) Áp dụng Định lý Pythagoras cho tam giác vuông ABH, ta có:
AB2=BH2+AH2=22+42=>AB=\(\sqrt{20}\)cm
Áp dụng Định lý Pythagoras cho tam giác vuông ACH, ta có:
AC2=AH2+CH2=42+82=>AC=\(\sqrt{80}\)cm
b) Xét \(\Delta\)ABC:AB<AC(Suy ra trực tiếp từ kết quả câu a)
Suy ra: B>C (Định lý về cạnh và góc đối diện trong tam giác)

C A E K B D
a) Xét tam giác ACE và tam giác AKE
có AE chung
góc CAE =góc KAE (GT)
góc ECA = góc EKA =900
suy ra tam giác ACE = tam giác AKE (cạnh huyền-góc nhọn) (1)
b) Từ (1) suy ra AC=AK suy ra A thuộc đường trung trực của CK (2)
Từ (1) suy ra EK=EC suy ra E thuộc đường trung trực của CK (3)
Từ(2) và (3) suy ra AE là đường trung trực của CK
c) tam giác ABC vuông tại C, có góc CAB = 600
suy ra AC=AB:2 ( cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)
mà AK=AC , AK +KB=AB
suy ra AK=AC=KB
d) tam giác BDE=tam giác BKE (cạnh huyền-góc nhọn)