Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

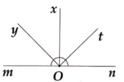

c) Từ đề bài, ta suy ra tia Oy và Om cùng thuộc nửa mặt phẳng bờ có chứa tia Ox; tia On và Ot thuộc nửa mặt phẳng còn lại có bờ chứa tia Ox. Vậy tia Ox nằm giữa hai tia Oy và Ot. Do đó, ta tính được góc y O t ^ = 90 ° .

a) Theo tính chất tia phân giác của một góc, ta có m O x ^ = m O n ^ 2 = 90 °
b) Tương tự ý a), ta có:
y O x ^ = 45 ° , x O t ^ = 45 °
Do đó, y O x ^ = x O t ^
c) Từ đề bài, ta suy ra tia Oy và Om cùng thuộc nửa mặt phẳng bờ có chứa tia Ox; tia On và Ot thuộc nửa mặt phẳng còn lại có bờ chứa tia Ox. Vậy tia Ox nằm giữa hai tia Oy và Ot. Do đó, ta tính được góc y O t ^ = 90°.

a) Ta có : ^mOn = 1800 ( vì ^mOn là góc bẹt)
Vì tia Ox là tia phân giác của ^mOn nên ^mOx = 1/2 ^mOn = 1/2.1800 = 900
Vậy ^mOx = 900
b) Vì Oy là tia phân giác của ^mOx nên ^mOy = ^yOx = 1/2 ^mOx = 1/2.900 = 450
Ta lại có : ^mOx = ^xOn = 900(vì hai góc này cùng vuông góc với tia Ox)
Vì Ot là tia phân giác của ^nOx nên ^xOt = ^tOn = 1/2.^xOn = 1/2.900 = 450
=> ^yOx = ^xOt = 450
c) Ta có : ^yOz + ^zOt = 450 + 450 = 900
P/S : K chắc :<
À quên cái khúc này :
c) Ta có : ^yOz + ^zOt = 450 + 450 = 900 = ^yOt
Vậy ^yOt = 900

Tính được:
a ) n O p ^ = 80 ° , t O p ^ = 40 ° . b ) m O t ^ = 120 °

a/ vì xoy > xot
=> ot là tia nằm giữa hai tia ox ,oy
b/ vì ot nằm giữa nên ta có hệ thức yot + tox = xoy
=> toy = xoy - tox
= 60 - 30 = 30 độ
=> toy = xot
c/ ot là tia pân giác xoy
vì yot + tox = xoy
yot = tox = 30 độ
d/ vì om là tia phân giác xot
=> tom = mox = tox : 2
= 30 : 2 = 15 độ
vì mot < toy
=> ot là tia nằm giữa hai tia om, oy
vậy moy = yot + tom
= 30 + 15 = 45 độ
Bài 2:
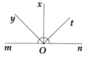
a: Ta có: Ox là tia phân giác của \(\widehat{mOn}\)
nên \(\widehat{mOx}=\widehat{nOx}=\dfrac{180^0}{2}=90^0\)
b: Ta có: Oy là tia phân giác của \(\widehat{mOx}\)
nên \(\widehat{yOx}=\dfrac{90^0}{2}=45^0\left(1\right)\)
Ta có: tia Ot là tia phân giác của \(\widehat{nOx}\)
nên \(\widehat{xOt}=\dfrac{90^0}{2}=45^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\widehat{xOy}=\widehat{xOt}\)