NM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
17 tháng 12 2018
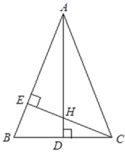
Kẻ đường cao AD. Xét ΔCBE và ΔABD có B E C ^ = A D B ^ = 90 ∘ và góc B chung nên ΔCBE ~ ΔABD (g.g) => B C A B = B E B D hay 18 A B = 6 , 75 9 => AB = 24cm.
Đáp án: C
6 tháng 6 2016
Câu a sử dụng tính chất đường phân giác trong tam giác
Câu b sử dụng tam giác đồng dạng
21 tháng 1 2023
a: Xét ΔABC có BM là phân giác
nên AM/AB=CM/BC
=>AM/15=CM/10
=>AM/3=CM/2=(AM+CM)/(3+2)=15/5=3
=>AM=9cm; CM=6cm
b: BM vuông góc BN
=>BN là phân giác góc ngoài tại B
=>NC/NA=BC/BA
=>NC/(NC+15)=10/15=2/3
=>3NC=2NC+30
=>NC=30cm
HC
31 tháng 8 2020
Bài 1 : Bài giải
A B C D E F O
a, Trong \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\text{ }\Rightarrow\text{ }9^2+12^2=81+144=225=BC^2\text{ }\Rightarrow\text{ }BC=5\text{ }cm\)
b, Vì BD là đường phân giác \(\widehat{ABC}\) nên : \(\widehat{B_1}=\widehat{B_2}\)
Xét 2 tam giác \(\Delta ABD\) vuông tại A và \(\Delta AED\) vuông tại E có :
\(BD\) : cạnh huyền - cạnh chung
\(\widehat{B_1}=\widehat{B_2}\) ( cmt )
\(\Rightarrow\text{ }\Delta ABD=\Delta AED\text{ }\left(ch-gn\right)\)
\(\Rightarrow\text{ }AD=DE\text{ }\left(2\text{ cạnh tương ứng }\right)\)
\(\Rightarrow\text{ }\Delta DAE\text{ cân }\)
c, Trong \(\Delta DEC\text{ }\) vuông tại E có : DC là cạnh đối diện với \(\widehat{E}\) nên \(DC\) là cạnh có độ dài lớn nhất \(\Rightarrow\text{ }DE< DC\)
Mà \(DA=DE\text{ nên }DA< DC\)
d, Vì \(\hept{\begin{cases}DE\text{ }\perp\text{ }BC\\BF\text{ }\perp\text{ }CF\\AB\text{ }\perp\text{ }AC\end{cases}}\text{ }\Rightarrow\text{ }DE\text{ , }AB\text{ và }BF\text{ là đường cao của }\Delta OBC\)
\(\Rightarrow\text{ }AB\text{, }DE\text{ và }CF\text{ đồng quy tại 1 điểm}\)
21 tháng 1 2023
a: Xét ΔABC có BM là phân giác
nên AM/AB=CM/BC
=>AM/15=CM/10
=>AM/3=CM/2=(AM+CM)/(3+2)=15/5=3
=>AM=9cm; CM=6cm
b: BM vuông góc BN
=>BN là phân giác góc ngoài tại B
=>NC/NA=BC/BA
=>NC/(NC+15)=10/15=2/3
=>3NC=2NC+30
=>NC=30cm
ai giúp mình gấp với😭
a) ta có AB = AC = 1CM (vì tam giác ABC cân tại A)
ta có : BC² = AB² + AC²
BC² = 1² + 1² = 1 + 1 = 2
BC = \(\sqrt{2}\)
b) ta có: AB² + AC² = BC²
mà AB = AC
=> 2AB² = BC² = \(\sqrt{18}^2=18\)
AB² = 9
AB = 3 (= AC)