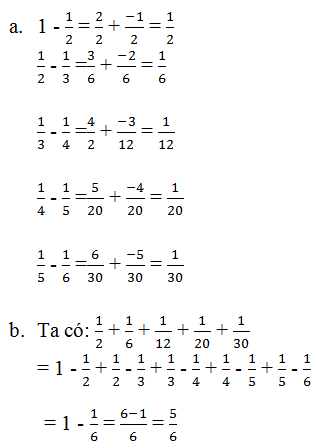Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=1+2\left(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{98.99}+\frac{1}{99.100}\right)\)
\(A=1+2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\right)\)
\(A=1+2\left(\frac{1}{2}-\frac{1}{100}\right)=1+2.\frac{49}{100}=1+\frac{49}{50}\)
\(A=\frac{99}{50}\)
Vậy \(A=\frac{99}{50}\)

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)

1)5x+1 + 6.5x+1 = 875
5x+1 ( 1+6 ) = 875
5x+1 . 7 = 875
5x+1 = 875 : 7
5x+1 = 125
5x+1 = 53
x+1 = 3
x = 3 - 1
x = 2
2)3x+1 + 3x+3 = 810
3x . 3 + 32 . 3x+1 = 810
3x . 3 + 9 . 3x . 3 = 810
3x .3 ( 1 + 9 ) = 810
3x+1 . 10 = 810
3x+1 = 810 : 10
3x+1 = 81
3x+1 = 34
x+1 = 4
x = 4-1
x = 3

\(\frac{1}{2}\) + \(\frac{1}{6}\) + \(\frac{1}{12}\) + ............ + \(\frac{1}{90}\) + \(\frac{1}{110}\)
= \(\frac{1}{1.2}\) + \(\frac{1}{2.3}\) + \(\frac{1}{3.4}\) + ............ + \(\frac{1}{9.10}\) + \(\frac{1}{10.11}\)
= 1 - \(\frac{1}{2}\) + \(\frac{1}{2}\) - \(\frac{1}{3}\) + \(\frac{1}{3}\) - \(\frac{1}{4}\) + ................. + \(\frac{1}{9}\) - \(\frac{1}{10}\) + \(\frac{1}{10}\) - \(\frac{1}{11}\)
= 1 - \(\frac{1}{11}\)
= \(\frac{10}{11}\)

\(G=\frac{1}{3^0}+\frac{1}{3^1}+...+\frac{1}{3^{2005}}\)\(\Rightarrow3G=3+\frac{1}{3^0}+\frac{1}{3^1}+\frac{1}{3^2}+...+\frac{1}{3^{2004}}\)
\(\Rightarrow3G-G=2G=3-\frac{1}{3^{2005}}\)\(\Rightarrow G=\frac{3-\frac{1}{3^{2005}}}{2}\)
\(Y=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2012}}\)\(\Rightarrow2Y=2+1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2011}}\)
\(\Rightarrow2Y-Y=2-\frac{1}{2^{2012}}\) \(\Rightarrow Y=2-\frac{1}{2^{2012}}\)