Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Công thức tính diện tích S của bồn hoa là: \(S = \pi .{R^2} = \pi .0,{8^2}\left( {{m^2}} \right)\)
b) Giá trị \(\left| {S - 1,984} \right|\) biểu diễn độ lệch giữa số “1,984” và S.

Chọn C.
+ Điểm trung bình của học sinh A:
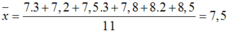
+ Điểm trung bình của học sinh B:
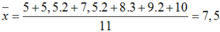


a) Dạng chuẩn của số π với 10 chữ số chắc là 3,141592654 với sai số tuyệt đối ∆π≤ 10-9.
b) Viết π ≈ 3,14 ta mắc phải sai số tuyệt đối không quá 0,002. Trong cách viết này có 3 chữ số đáng tin.
Viết π ≈ 3,1416 ta mắc phải sai số tuyệt đối không quá 10-4. Viết như vậy thì số π này có 5 chữ số đáng tin.

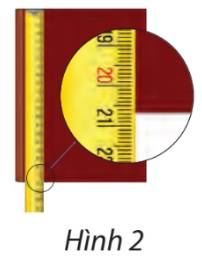
Quan sát Hình 2, ta thấy: Chiều dài trang bìa sổ gần tới vạch thứ 7 giữa số 20 và 21.
Do đó quyển sổ dài gần 20,7 cm.
Vậy kết quả của bạn Hoa có sai số nhỏ hơn.

Ta có: \(1,41 < \sqrt 2 < 1,42\) hay \(1,415 - 0,005 < \sqrt 2 < 1,415 + 0,005\)
\( \Rightarrow \) Số gần đúng của \(\sqrt 2 \) là 1,415 với độ chính xác 0,005
Khi đó: Độ dài đường chéo của hình vuông cạnh 10 cm là: \(10.1,415 = 14,15\;(cm)\)
Độ dài đúng là \(10\sqrt 2 \)cm, thỏa mãn: \(10.1,41 < 10\sqrt 2 < 10.1,42\) hay \(14,1 < 10\sqrt 2 < 14,2\)
Do đó \(14,1 - 14,15 < 10\sqrt 2 - 14,15 < 14,2 - 14,15\), tức là \(\left| {10\sqrt 2 - 14,15} \right| < 0,05.\)
Vậy kết quả 14,15 cm có độ chính xác là 0,05.

a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
.(3x5 + 7x6 + 12x7 + 14x8 + 3x9 + 1x10) = 7,25
.(8x6+18x7+10x8+4x9) = 7,25.
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
= 1,2875
= 0,7875.
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.

a) Kết quả trung bình của Cung thủ A là:
\(\frac{{8 + 9 + 10 + 7 + 6 + 10 + 6 + 7 + 9 + 8}}{{10}} = 8\)
Kết quả trung bình của Cung thủ A là:
\(\frac{{10 + 6 + 8 + 7 + 9 + 9 + 8 + 7 + 8 + 8}}{{10}} = 8\)
b)
+) Khoảng biến thiên số điểm của cung thủ A là: \(R = 10 - 6 = 4\)
Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}6&6&7&7&8&8&9&9&{10}&{10}\end{array}\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 8.\)
Tứ phân vị thứ nhất là trung vị của mẫu:\(6,6,7,7,8\). Do đó \({Q_1} = 7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(8,9,9,10,10\). Do đó \({Q_3} = 9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 9 - 7 = 2\)
+) Khoảng biến thiên số điểm của cung thủ A là: \(R = 10 - 6 = 4\)
Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}6&7&7&8&8&8&8&9&9&{10}\end{array}\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 8.\)
Tứ phân vị thứ nhất là trung vị của mẫu:\(6,6,7,7,8\). Do đó \({Q_1} = 7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(8,9,9,10,10\). Do đó \({Q_3} = 9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 9 - 7 = 2\)
=> Nếu so sánh khoảng chênh lệch và khoảng tứ phân vị thì không xác định được kết quả của cung thủ nào ổn định hơn.
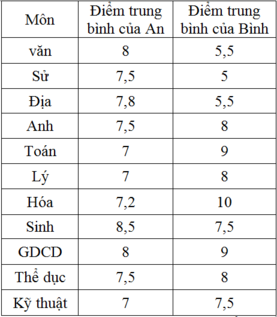

a) Vì công thức chu vi đường tròn là \(2\pi R\) với R là độ dài bán kính, trong đó \(\pi \) là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.
b)
Kết quả của An: \({S_1} = 2\pi R \approx 2.3,14.2 = 12,56\) cm:
Kết quả của Bình: \({S_2} = 2\pi R \approx 2.3,1.2 = 12,4\)cm.
Ta thấy \(\pi > 3,14 > 3,1 => 2.\pi. R > {S_1} > {S_2}\)
\( = > \left| {2\pi R - {S_1}} \right| < \left| {2\pi R - {S_2}} \right|\)
Nói cách khác, sai số tuyệt đối của \(S_1\) nhỏ hơn \(S_2\).
=> Kết quả của An chính xác hơn.