Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
a) +) ta co: tam giác GLO
GL = 6, LO = 8, OG = 10
=> GL < LO < GO ( 6<8<10)
=> góc O < góc G < góc L ( quan hệ giữa góc và cạnh đối diện trong tam giác LOG )
+) ta co: tam giac UVW
góc V = 40, góc U = 50
=> góc W = 180 - ( góc V + goc Ư )
= 180 - ( 50 + 40)
= 90
=> góc V < góc U < góc W
=> UW < VW < VU ( quan hệ giữa cạnh và góc trong tam giác ACB )

Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)

A C B O
a) Trong tam giác BOC có cạnh BC lớn nhất.
b) Theo đề bài, ta có:
OB<OC
=>\(\widehat{OCB}\)< \(\widehat{OBC}\)
Mặc khác, ta có:
\(\widehat{ACB}\)=\(\widehat{ACO}\)+ \(\widehat{OCB}\)=2.\(\widehat{OCB}\)
\(\widehat{ABC}\)=\(\widehat{ABO}\)+\(\widehat{OBC}\)=2.\(\widehat{OBC}\)
Mà \(\widehat{OCB}\)< \(\widehat{OBC}\)
=>2.\(\widehat{OCB}\)<2.\(\widehat{OBC}\)
hay:\(\widehat{ACB}\)<\(\widehat{ABC}\)

\(\left(\dfrac{-5}{13}\right)^{2017}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(\dfrac{-5}{13}\right)\cdot\left(-\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(\dfrac{-5}{13}\right)\cdot\left(\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}=\left(-\dfrac{5}{13}\right)\cdot\left[\left(\dfrac{5}{13}\right)^{2016}\cdot\left(\dfrac{13}{5}\right)^{2016}\right]=\left(-\dfrac{5}{13}\right)\cdot1^{2016}=\left(-\dfrac{5}{13}\right)\cdot1=-\dfrac{5}{13}\)

Giải:
Theo đề ra, ta có:
\(3x=-2y\Leftrightarrow\dfrac{x}{-2}=\dfrac{y}{3}\)
Và \(2x+y=5\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{-2}=\dfrac{y}{3}=\dfrac{2x}{-4}=\dfrac{2x+y}{-4+3}=\dfrac{5}{-1}=-5\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{-2}=-5\\\dfrac{y}{3}=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5.\left(-2\right)\\y=-5.3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=-15\end{matrix}\right.\)
Vậy \(x=10\) và \(y=-15\).
Chúc bạn học tốt!!!
\(3x=-2y\)
=>\(\dfrac{x}{-2}=\dfrac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{-2}=\dfrac{y}{3}=\dfrac{2x+7}{2.\left(-2\right)+3}=\dfrac{5}{-1}=-5\)
=>\(x=\left(-5\right).\left(-2\right)=10\)
\(y=-5.3=-15\)
Vậy...

Ta có hình vẽ:
x x' O y y' \(\widehat{xOy}+\widehat{yOx'}+\widehat{x'Oy'}=297^o\)
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh \(\Rightarrow\widehat{xOy}=\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{x'Oy'}\) kề bù nên:
\(\widehat{x'Oy'}+\widehat{x'Oy}=180^o\)
\(\Rightarrow\widehat{xOy}+180^0=297^o\)
\(\Rightarrow\widehat{xOy}=117^o\)
\(\widehat{xOy}=\widehat{x'Oy'}=117^o\)
\(\Rightarrow\widehat{x'Oy}=297^o-117^o-177^o=3^o\)
\(\widehat{x'Oy}\) đối đỉnh với \(\widehat{xOy'}\) nên
\(\widehat{x'Oy}=\widehat{xOy'}=3^o\)
Vậy...


Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của ΔABC và ΔA’B’C’ ta viết:
∆ABC= ∆A’B’C’.
∆ABC= ∆A’B’C’ nếu
Hướng dẫn giải bài tập SGK bài 2 tam giác bằng nhau trang 111, 112.
Bài 10. Trong các hình sau các Δ nào bằng nhau(Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các Δ bằng nhau đó. Viết kí hiệu về sự bằng nhau của các Δ đó.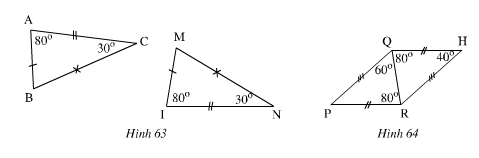
Hình 63:
Ta có:
Xét ΔABC ta có: ∠B =1800 – (∠A+∠C)=1800 – (800+300) =700
Xét ΔMIN ta có: ∠M =1800 – (∠I+∠N)=1800 – (800+300) =700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC = ∆IMN
Hình 64:
Ta có:
∠RQH = ∠QRP = 800 (ở vị trí so le trong)
Nên QH // RP
Nên ∠HRQ = ∠PQR = 600(so le trong)
∠P = ∠H = 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR = ∆PRQ.
Bài 11. Cho ∆ ABC = ∆ HIK
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với ∠H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.
HD: a) Ta có ∆ ABC = ∆ HIK, nên cạnh tương ứng với BC là cạnh IK. Góc tương ứng với ∠H là ∠A.
b) ∆ ABC= ∆ HIK
Suy ra: AB = HI, AC = HK, BC = IK.
∠A = ∠H, ∠B =∠I, ∠C = ∠K.
Luyện tập: Giải bài 12, 13, 14 trang 112 Toán 7 tập 1 (hình học)
Bài 12 trang 112. Cho ∆ ABC= ∆ HIK trong đó cạnh AB = 2cm. ∠B=400; BC= 4cm. Em có thể suy ra số đo của những cạnh nào, những góc nào của ΔHIK?
Ta có ∆ ABC= ∆ HIK (gt)
Suy ra: AB = HI= 2cm, BC = IK= 4cm, ∠I = ∠B = 400
Bài 13. Cho ∆ ABC= ∆ DEF. Tính chu vi mỗi tam giá nói trên biết AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó)
Ta có ∆ABC = ∆ DEF
Suy ra: AB = DE= 4cm, BC = EF = 6cm, DF = AC = 5cm.
Chu vi của ΔABC bằng: AB + BC + AC = 4 + 5 + 6 = 15 (cm)
Chu vi của ΔDEF bằng: DE + EF + DF = 4 + 5 + 6 = 15 (cm )
Bài 14 trang 112. Cho hai tam giác bằng nhau: ΔABC (Không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một Δ có ba đỉnh H, I ,K. Viết kí hiệu về sự bằng nhau của hai Δ đó biết: AB=KI, ∠B =∠K.
Giải: Ta có: ∠B =∠K nên B, K là hai đỉnh tương ứng.
AB= KI nên A, I là hai đỉnh tương ứng.
Vậy ∆ABC = ∆IKH.