Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác AEDF có: góc A = góc E = góc F= 90 độ
mà AD là tia phân giác của góc AED => AEDF là hình vuông
b) Xét tam giác vuông ABH có: góc HBA + góc BAH =90 độ
Xét tam giác vuông ABC có : góc ABH + góc ACB=90 mà góc HBA = góc ABH => góc BAH = góc ACB (1)
AM là đường trung tuyến ứng với cạnh huyền của tam giác vuông ABC
=> AM=1/2 BC = MC =.> AMC là tam giác cân tại M =>góc MAC=góc ACB
mà góc ACB= góc BAH (10=> góc MAC= góc BAH
Mà góc BAD=góc DAC => góc HAD = góc MAD => AD là tia phân giác của góc MAH

a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
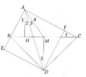

Hình tự túc, bùn ngủ => ko vẽ nữa.
a) Ta có: AC _|_ AB ; HE _|_ AB => AC // HE
=> FHA^ = EAH^ (sole trong)
FAH^ = EHA^ (sole trong)
Xét \(\Delta\)FAH và \(\Delta\)EHA :
FHA^ = EAH^
AH chung
FAH^ = EHA^
=> \(\Delta\)FAH = \(\Delta\)EHA (g.c.g)
=> FA = EH (2 cạnh tương ứng)
Xét \(\Delta\)FAE và \(\Delta\)HEA:
FAE^ = HEA^ =90o
FA = EH (cmt)
AE chung
=> \(\Delta\)FAE = \(\Delta\)HEA (2 cạnh góc vuông)
=> FE = HA (2 cạnh tương ứng)
b) Bn ơi, chữ EI hơi lạ. Xem lại nhé.
