Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta nhân rồi chia cả 2 vế cho 64.12
Có: 48 . 12 = 576
Ta lấy 576 : (64 . 12) = \(\dfrac{{576}}{{768}}\)
Bên cạnh đó, ta thấy ước chung lớn nhất của tử và mẫu là 192 nên ta rút gọn phân số \(\dfrac{{576:192}}{{768:192}} = \dfrac{3}{4}\)
Xét vế trái 64 . 9 = 576 ta lấy 567 : (64 . 12) = \(\dfrac{{576}}{{768}} = \dfrac{3}{4}\)
Như vậy sau khi chia cả 2 vế cho 64 . 12 ta được kết quả là cả 2 vế bằng nhau và cùng bằng \(\dfrac{3}{4}\)
- Từ đẳng thức ad = cb ta chia cả 2 vế cho bd sẽ được \(\dfrac{{ad}}{{bd}} = \dfrac{{bc}}{{bd}} \Leftrightarrow \dfrac{a}{b} = \dfrac{c}{d}\)

\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}+1=\dfrac{c}{d}+1=>\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}-1=\dfrac{c}{d}-1=>\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>ad=cb=>ad+ac=cb+ac\)
\(=>a\left(c+d\right)=c\left(a+b\right)=>\dfrac{a}{c}=\dfrac{a+b}{c+d}=>\dfrac{a}{a+b}=\dfrac{c}{c+d}\)

\(\Leftrightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a}{c}=\dfrac{b}{d}=>\dfrac{a}{b}=\dfrac{c}{d}\)
Lời giải:
$\frac{a+b}{a-b}=\frac{c+d}{c-d}$
$\Rightarrow (a+b)(c-d)=(a-b)(c+d)$
$\Rightarrow ac-ad+bc-bd=ac+ad-bc-bd$
$\Rightarrow 2ad=2bc$
$\Rightarrow ad=bc$
$\Rightarrow \frac{a}{b}=\frac{c}{d}$ (đpcm)

a) Ta có: 6. (-15) = -90;
10.(-9) = = - 90
Vậy tích hai số hạng 6 và -15 bằng tích hai số hạng 10 và -9
b) Nhân hai vế của tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với tích bd, ta được: \(\frac{{a.b.d}}{b} = \frac{{c.b.d}}{d} \Rightarrow ad = bc\)
Vậy ta được đẳng thức ad = bc
a) 6.(-15) = 10.(-9) = -90
b) a/b . bd = ad
c/d . bd = bc
Ta được ad = bc

Ta có : \(\dfrac{a}{b}=\dfrac{c}{d}\) suy ra \(\dfrac{a}{c}=\dfrac{b}{d}\)
Theo tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Suy ra: \(\dfrac{a+b}{a-c}=\dfrac{c+d}{c-d}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk\) và \(c=dk\)
Nên \(\dfrac{a+b}{c-d}=\dfrac{bk+b}{dk-d}=\dfrac{b\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\Rightarrow\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) (với \(a-b\ne0,c-d\ne0\))
Vậy \(\dfrac{a}{b}=\dfrac{c}{d}thì\)\(\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) ( \(a-b\ne0,c-d\ne0\))

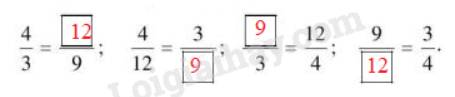
a: \(4\cdot\dfrac{9}{9\cdot3}=\dfrac{4}{3};3\cdot\dfrac{12}{9\cdot3}=\dfrac{12}{9}=\dfrac{4}{3}\)
b: 4/3=12/9
4/12=3/9
9/3=12/4
9/12=3/4

Ta có: \(\dfrac{a}{b} = \dfrac{c}{d}\) nên a.d = b.c
Ta suy ra được các tỉ lệ thức: \(\dfrac{a}{c} = \dfrac{b}{d};\dfrac{d}{b} = \dfrac{c}{a};\dfrac{d}{c} = \dfrac{b}{a}\)
\(\dfrac{a}{c}=\dfrac{b}{d}\\ \dfrac{a}{d}=\dfrac{c}{b}\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk,c=dk\)
Ta có: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\left(k-1\right)}=\dfrac{k+1}{k-1}\) (1)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
Ta có: \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\).Theo tính chất của dãy tỉ số bằng nhau:
\(\Rightarrow\)\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=\(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)
Vì \(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)\(\Leftrightarrow\)\(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
Vậy \(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
Nếu bạn muốn làm cách cơ bản thì hãy làm theo mình.Còn nếu bạn học toán nâng cao thì làm theo cách bạn Linh hay hơn.Chúc bạn học tốt

a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)



a) \(\dfrac{{48}}{{64}} = \dfrac{9}{{12}}\)ta nhân cả 2 vế cho 64.12 được : \(\dfrac{{48}}{{64}}.(64.12) = \dfrac{9}{{12}}.(64.12)\)
\( \Rightarrow \)\(\dfrac{{48.64.12}}{{64}} = \dfrac{{9.64.12}}{{12}}\)\( \Rightarrow \)\(48.12\)= \(9.64\) \( \Leftrightarrow \) 576 = 48.12 = 9.64
\( \Rightarrow \) Ta thấy nhân cả 2 vế với 64.12 ta được 2 vế sau khi rút gọn bằng nhau
b) \(\dfrac{a}{b} = \dfrac{c}{d}\) nhân cả 2 vế với b.d ta có : \(\dfrac{{a \cdot b \cdot d}}{b} = \dfrac{{c \cdot b.d}}{d}\) sau khi rút gọn cả 2 vế ta được : a.b = c.d