Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x^3+1\right)-\left(x^3-1\right)\)
\(=x^3+1-x^3+1\)
\(=2\)
Biểu thức trên có giá trị bằng 2 với mọi x nên không phụ thuộc vào biến.
b) \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)-\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)-27\left(2y^3-1\right)\)
\(=\left(8x^3+27y^3\right)-\left(8x^3-27y^3\right)-27\left(2y^3-1\right)\)
\(=8x^3+27y^3-8x^3+27y^3-54y^3+27\)
\(=27\)
Biểu thức trên có giá trị bằng 27 với mọi x nên không phụ thuộc vào biến.
c) \(\left(x-1\right)^3-\left(x+4\right)\left(x^2-4x+16\right)+3x\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-64+3x^2-3x\)
\(=-65\)
Biểu thức trên có giá trị bằng -65 với mọi x nên không phụ thuộc vào biến.
d) \(\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2-3\left(x^2+y^2+z^2\right)\)
\(=x^2+y^2+z^2+2\left(xy+yz+xz\right)+\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2-3\left(x^2+y^2+z^2\right)\)
\(=2\left(xy+yz+xz\right)-2\left(x^2+y^2+z^2\right)+x^2-2xy+y^2+x^2-2xz+z^2+y^2-2yz+z^2\)
\(=2\left(xy+yz+xz\right)-2\left(x^2+y^2+z^2\right)+2\left(x^2+y^2+z^2\right)-2\left(xy+yz+xz\right)\)
\(=0\)
Biểu thức trên có giá trị bằng 0 với mọi x nên không phụ thuộc vào biến.

a)
\(5x(x-2y)+2(2y-x)^2=5x(x-2y)+2(x-2y)^2\)
\(=(x-2y)[5x+2(x-2y)]=(x-2y)(7x-4y)\)
b)
\(7x(y-4)^2-(4-y)^3=7x(y-4)^2+(y-4)^3=(y-4)^2(7x+y-4)\)
c)
\((4x-8)(x^2+6)-(4x-8)(x+7)+9(8-4x)\)
\(=(4x-8)(x^2+6)-(4x-8)(x+7)-9(4x-8)\)
\(=(4x-8)[(x^2+6)-(x+7)-9]=(4x-8)(x^2-x-10)=4(x-2)(x^2-x-10)\)
d)
\(x^2-xz-9y^2+3yz=(x^2-9y^2)-(xz-3yz)\)
\(=(x-3y)(x+3y)-z(x-3y)=(x-3y)(x+3y-z)\)
e)
\(x^2(x^2-6)-x^2+9=x^4-7x^2+9=(x^4-6x^2+9)-x^2\)
\(=(x^2-3)^2-x^2=(x^2-3-x)(x^2-3+x)\)
a)
\(5x(x-2y)+2(2y-x)^2=5x(x-2y)+2(x-2y)^2\)
\(=(x-2y)[5x+2(x-2y)]=(x-2y)(7x-4y)\)
b)
\(7x(y-4)^2-(4-y)^3=7x(y-4)^2+(y-4)^3=(y-4)^2(7x+y-4)\)
c)
\((4x-8)(x^2+6)-(4x-8)(x+7)+9(8-4x)\)
\(=(4x-8)(x^2+6)-(4x-8)(x+7)-9(4x-8)\)
\(=(4x-8)[(x^2+6)-(x+7)-9]=(4x-8)(x^2-x-10)=4(x-2)(x^2-x-10)\)
d)
\(x^2-xz-9y^2+3yz=(x^2-9y^2)-(xz-3yz)\)
\(=(x-3y)(x+3y)-z(x-3y)=(x-3y)(x+3y-z)\)
e)
\(x^2(x^2-6)-x^2+9=x^4-7x^2+9=(x^4-6x^2+9)-x^2\)
\(=(x^2-3)^2-x^2=(x^2-3-x)(x^2-3+x)\)

\(a,3x^3y^3-15x^2y^2=3x^2y^2\left(xy-5\right)\)
\(b,5x^3y^2-25x^2y^3+40xy^4\)
\(=5xy^2\left(x^2-5xy+8y^2\right)\)
\(c,-4x^3y^2+6x^2y^2-8x^4y^3\)
\(=-2x^2y^2\left(2x-3+4x^2y\right)\)
\(d,a^3x^2y-\frac{5}{2}a^3x^4+\frac{2}{3}a^4x^2y\)
\(=a^3x^2\left(y-\frac{5}{2}x^2+\frac{2}{3}ay\right)\)
\(e,a\left(x+1\right)-b\left(x+1\right)=\left(x+1\right)\left(a-b\right)\)
\(f,2x\left(x-5y\right)+8y\left(5y-x\right)\)
\(=2x\left(x-5y\right)-8y\left(x-5y\right)=\left(x-5y\right)\left(2x-8y\right)\)
\(g,a\left(x^2+1\right)+b\left(-1-x^2\right)-c\left(x^2+1\right)\)
\(=\left(x^2+1\right)\left(a-b-c\right)\)
\(h,9\left(x-y\right)^2-27\left(y-x\right)^3\)
\(=9\left(x-y\right)^2+27\left(x-y\right)^3\)
\(=9\left(x-y\right)^2\left(1+3x-3y\right)\)
a,3x3y3−15x2y2=3x2y2(xy−5)a,3x3y3−15x2y2=3x2y2(xy−5)
b,5x3y2−25x2y3+40xy4b,5x3y2−25x2y3+40xy4
=5xy2(x2−5xy+8y2)=5xy2(x2−5xy+8y2)
c,−4x3y2+6x2y2−8x4y3c,−4x3y2+6x2y2−8x4y3
=−2x2y2(2x−3+4x2y)=−2x2y2(2x−3+4x2y)
d,a3x2y−52a3x4+23a4x2yd,a3x2y−52a3x4+23a4x2y
=a3x2(y−52x2+23ay)=a3x2(y−52x2+23ay)
e,a(x+1)−b(x+1)=(x+1)(a−b)e,a(x+1)−b(x+1)=(x+1)(a−b)
f,2x(x−5y)+8y(5y−x)f,2x(x−5y)+8y(5y−x)
=2x(x−5y)−8y(x−5y)=(x−5y)(2x−8y)=2x(x−5y)−8y(x−5y)=(x−5y)(2x−8y)
g,a(x2+1)+b(−1−x2)−c(x2+1)g,a(x2+1)+b(−1−x2)−c(x2+1)
=(x2+1)(a−b−c)=(x2+1)(a−b−c)
h,9(x−y)2−27(y−x)3h,9(x−y)2−27(y−x)3
=9(x−y)2+27(x−y)3

Bài 1 :
a ) \(2x\left(x+1\right)+2\left(x+1\right)=\left(x+1\right)\left(2x+2\right)=2\left(x+1\right)^2\)
b ) \(y^2\left(x^2+y\right)-zx^2-zy=y^2\left(x^2+y\right)-z\left(x^2+y\right)=\left(x^2+y\right)\left(y^2-z\right)\)
c ) \(4x\left(x-2y\right)+8y\left(2y-x\right)=4x\left(x-2y\right)-8y\left(x-2y\right)=4\left(x-2y\right)^2\)
d ) \(3x\left(x+1\right)^2-5x^2\left(x+1\right)+7\left(x+1\right)=\left(x+1\right)\left(3x^2+3x-5x^2+7\right)=\left(x+1\right)\left(3x-2x^2+7\right)\)
e ) \(x^2-6xy+9y^2=\left(x-3x\right)^2\)
Bài 1 :
f ) \(x^3+6x^2y+12xy^2+8y^3=\left(x+2y\right)^3\)
g ) \(x^3-64=\left(x-4\right)\left(x^2+4x+16\right)\)
h ) \(125x^3+y^6=\left(5x+y^2\right)\left(25x^2-5xy^2+y^4\right)\)
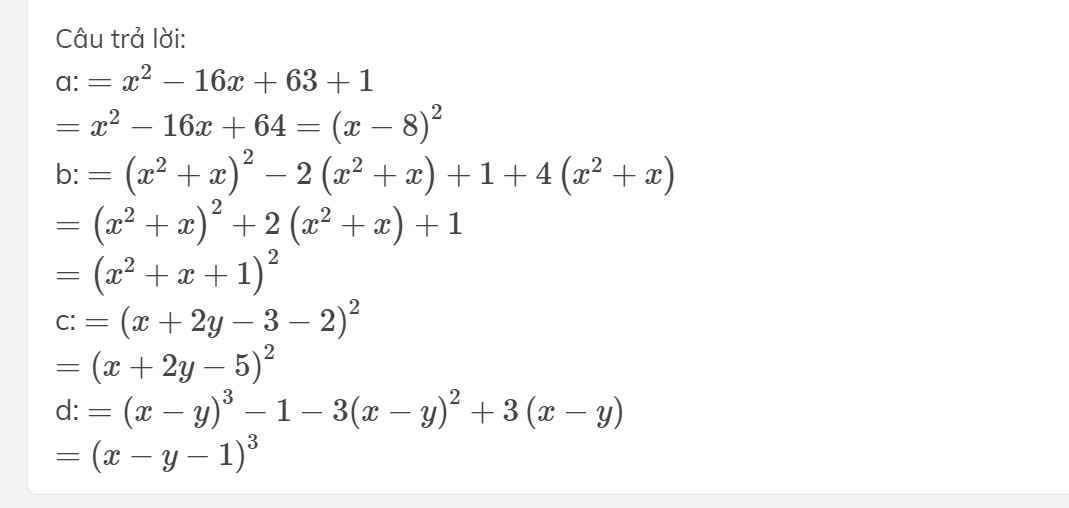
a)\(=\left(x^2-7x-9x+63\right)+1\)
\(=x^2-7x-9x+63+1\)
=\(x^2-16x+64\)
\(=\left(x-8\right)^2\)
a: \(=x^2-16x+63+1\)
\(=x^2-16x+64=\left(x-8\right)^2\)
b: \(=\left(x^2+x\right)^2-2\left(x^2+x\right)+1+4\left(x^2+x\right)\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+1\)
\(=\left(x^2+x+1\right)^2\)
c: \(=\left(x+2y-3-2\right)^2\)
\(=\left(x+2y-5\right)^2\)
d: \(=\left(x-y\right)^3-1-3\left(x-y\right)^2+3\left(x-y\right)\)
\(=\left(x-y-1\right)^3\)