K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG
4

16 tháng 7 2017
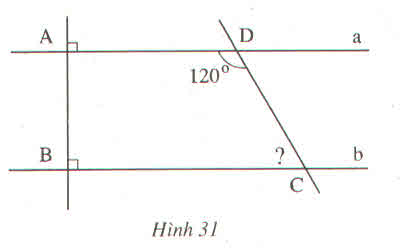
a, Ta có:
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
b, Ta có: a // b( câu a)
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)

LT
12 tháng 5 2017
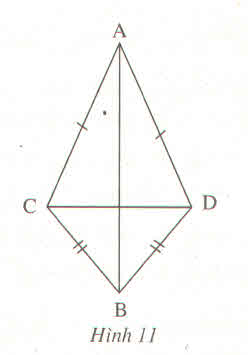
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD
SG
1

TT
20 tháng 4 2017
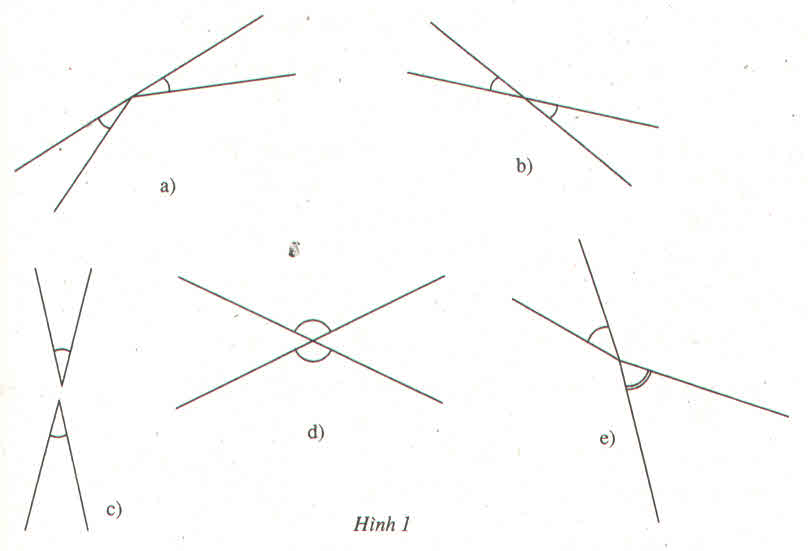
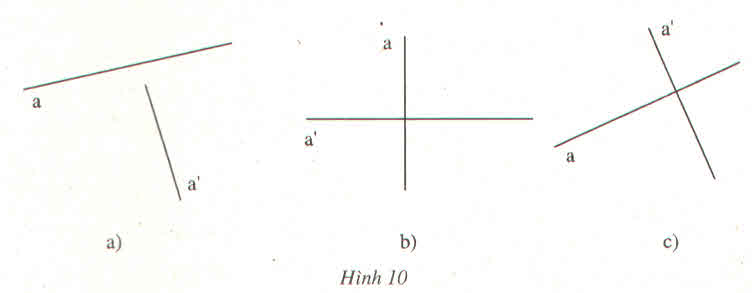
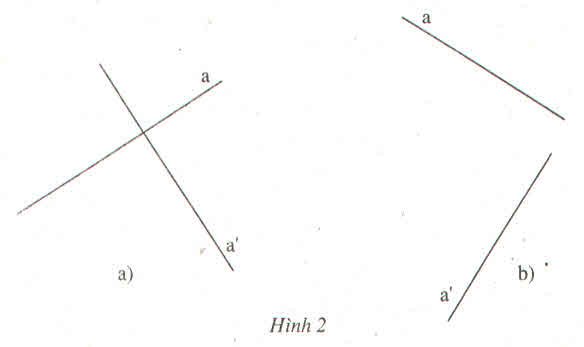
các đường thẳng a và a' ở hình 10 (a, b, c) có vuông góc với nhau
SG
1

5 tháng 7 2017
có, trong câu a và b: hai đường thẳng a và a' đều vuông góc với nhau. câu b bạn chỉ cần kéo dài 2 đường thẳng ra rồi dùng ê ke kiểm tra là thấy vuông đấy. ![]()
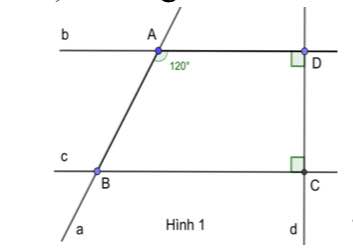










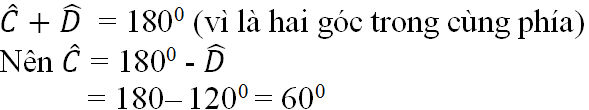
a, Vì b và c cùng vuông góc với d nên b//c
b, Vì b//c nên \(\widehat{A}=\widehat{ABc}=120^0\left(so.le.trong\right);\widehat{A}=\widehat{BCa}=120^0\left(đồng.vị\right)\)
Ta có \(\widehat{ABc}+\widehat{ABC}=180^0\left(kề.bù\right)\Rightarrow\widehat{ABC}=180^0-120^0=60^0\)
Ta có \(\widehat{aBc}=\widehat{ABC}=60^0\left(đối.đỉnh\right)\)
vì b//c
=> \(\widehat{DAB}+\widehat{ABC}=180\) ( 2 góc trong cùng phía bù nhau )
=> \(120+\widehat{ABC}=180=>\widehat{ABC}=60\)
=> \(\widehat{ABC}=\widehat{cBa}=60\) ( đối đỉnh)
\(\widehat{ABC}+\widehat{ABc}=180\) ( 2 góc kề bù)
=> \(60+\widehat{ABc}=180=>\widehat{ABc}=120\)
\(\widehat{ABc}=\widehat{aBC}=120\) đối đỉnh