PP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
-0,75)
=21/10
GIÚP MỊ NHA !!! TKS NHÌU 
HO
11 tháng 7 2017
tự vẽ hình nhé
giải
a/ do BM//AD nên =>
DAB=MBA (vì AD=BM)
b/ Do I là trung điểm của AB vàM là trung điểm của BC nên
=> I thẳng hàng với M
Ta có: AD // BM nên
=> D thẳng hàng với I
Do I thẳng hàng với M
mà D thẳng hàng với I
nên => Cả 3 điểm thẳng hàng với nhau
c/ Do 3 điểm thẳng hàng với nhau nên
=> BD // AM
12 tháng 7 2017
A B C . M / / . I // // D /
a) Vì AD // BM
=> \(\widehat{DAB}=\widehat{MBA}\left(soletrong\right)\)
Xét \(\Delta DAB\) và \(\Delta MBA\) có:
DA = BM (gt)
\(\widehat{DAB}=\widehat{MBA}\left(cmt\right)\)
AB (chung)
Do đó: \(\Delta DAB=\Delta MBA\left(c-g-c\right)\)
b) Vì \(\Delta DAB=\Delta MBA\left(cmt\right)\)
=> \(\widehat{DBA}=\widehat{MAB}\) (hai cạnh tương ứng)
Xét \(\Delta DIB\) và \(\Delta MIA\) có:
BI = IA (I là trung điểm của AB)
\(\widehat{DIB}=\widehat{MIA}\left(đđ\right)\)
\(\widehat{DBI}=\widehat{IAM}\left(\widehat{DBA}=\widehat{MAB}\right)\)
Do đó: \(\Delta DIB=\Delta MIA\left(g-c-g\right)\)
=> DI = IM (hai cạnh tương ứng)
Ta có: \(\widehat{DIB}=\widehat{MIA}\left(đđ\right)\)
mà \(\widehat{DIB}+\widehat{DIA}=180^0\) (B; I; A thẳng hàng)
=> \(\widehat{DIA}+\widehat{MIA}=180^0\)
hay \(\widehat{DIM}=180^0\)
=> D; I; M thẳng hàng
c) Vì \(\widehat{DBA}=\widehat{MAB}\left(cmt\right)\)
=> BD // AM
6 tháng 10 2017
x O y A B C
a) Ta có OA là tia phân giác của góc xOy
=>\(\widehat{COA}=\widehat{AOB}=\dfrac{xOy}{2}\)
\(\Rightarrow\widehat{COA}=\widehat{AOB}=\dfrac{60}{2}\)
\(\Rightarrow\widehat{COA}=\widehat{AOB}=30^0\)
b) Ta có \(OB//AC\)\(\Rightarrow\widehat{AOB}=\widehat{OAC}=30^0\)( 2 góc so le trong )
\(OC//AB\Rightarrow\widehat{OAC}=\widehat{BAO}=30^0\)( 2 góc so le trong )
c) Vì \(\widehat{OAC}=\widehat{BAO}=30^0\Rightarrow AO\)là phân giác của \(\widehat{BAC}\)
7 tháng 10 2017
a) góc so le trong là XOA =OAB
b)XOA=AOB ( OA là tia phân giác góc O)
mặt khác AOB=OAB từ đó => BOA=BAO
SG
1
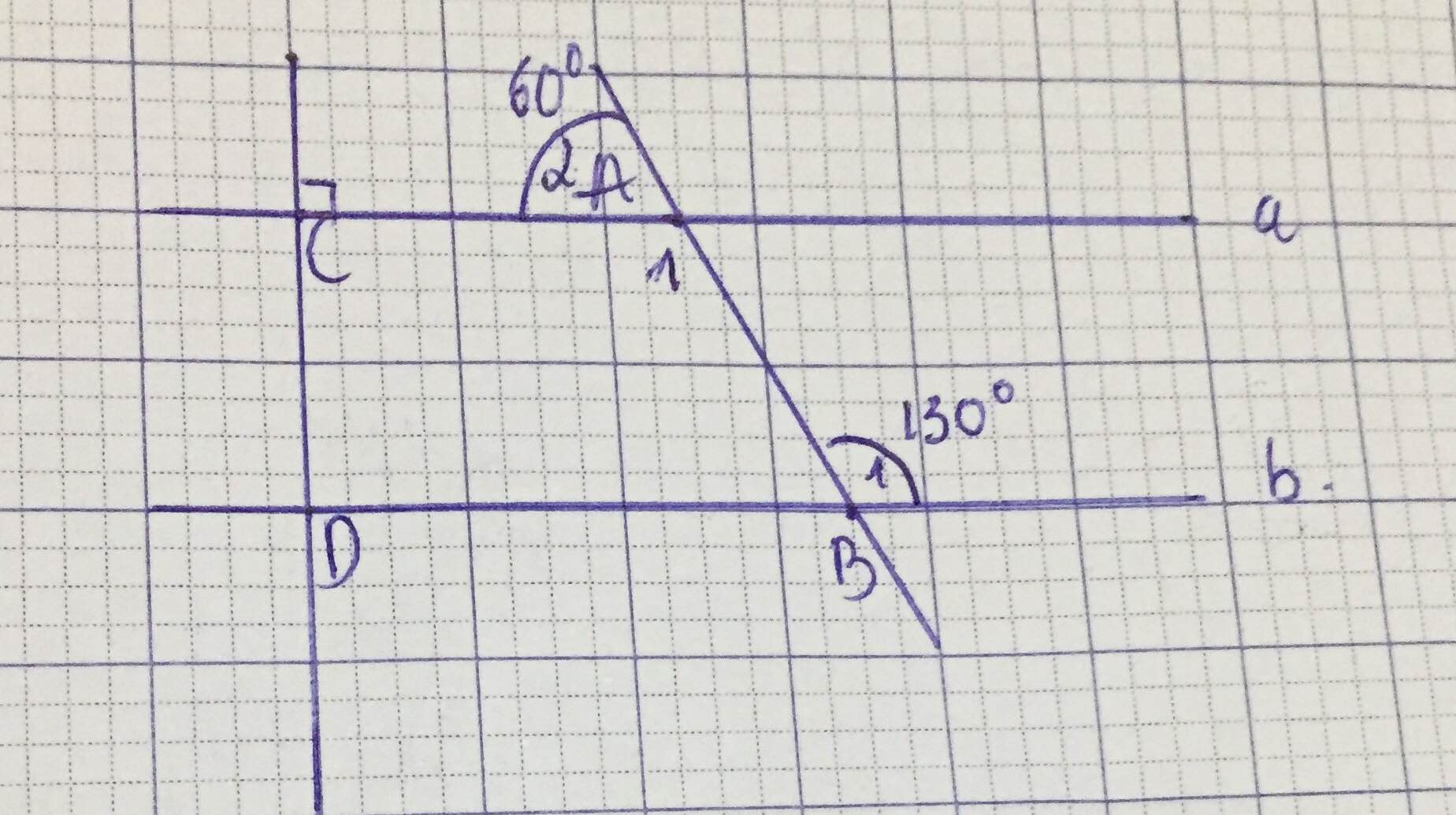
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)