Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.
Do đó, AM có là đường trung tuyến của tam giác ABC
- Ta có:
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)

tam giác ABC có : BE; CF là trung tuyến và cắt nhau tại I
=> AI là trung tuyến (tc)
mà tam giác ABC cân tại A (Gt)
=> AI là phân giác của góc BAC (đl)
a)Xét\(\Delta ABC\)có:\(BE\)là đg trung tuyến xuất phát từ đỉnh\(B\left(GT\right)\)
\(CF\)là đg trung tuyến xuất phát từ đỉnh\(C\left(GT\right)\)
mà\(BE\)cắt\(CF\)tại\(I\)
\(\Rightarrow AI\)là đg trung tuyến xuất phát từ đỉnh\(A\)(Định lí về tính chất 3 đg trung tuyến của 1\(\Delta\))
mà\(\Delta ABC\)cân tại\(A\left(GT\right)\)
\(\Rightarrow AI\)vừa là đg trung tuyến vừa là đg p/g của\(\Delta ABC\)(Tính chất của tg cân)
b)Xét\(\Delta ABI\)và\(\Delta ACI\)có:
\(AI\)là cạnh chung
\(\widehat{BAI}=\widehat{CAI}\)(\(AI\)là tia p/g của\(\widehat{BAC}\))
\(AB=AC\)(\(\Delta ABC\)cân tại\(A\))
Do đó:\(\Delta ABI=\Delta ACI\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{ACI}\)(2 cạnh t/ứ)
\(BI=CI\)(2 cạnh t/ứ)
Xét\(\Delta ABE\)và\(\Delta ACF\)có:
\(\widehat{ABE}=\widehat{ACF}\left(cmt\right)\)
\(AB=AC\)(\(\Delta ABC\)cân tại\(A\))

Ba đường trung tuyến của tam giác này có cùng đi qua một điểm

a) DE // AB, DE = \(\dfrac{1}{2}\)AB, IK // AB, IK = \(\dfrac{1}{2}\)AB
=> DE//IK và DE = IK
b) Xét tg GDE và tg GIK có:
DE = IK (cmt)
GDE = GIK (slt)
GED = GKI (slt)
=> tg GDE = tg GIK (g.c.g)
=> GD = GI ( c.t.ứ)
Có GD = GI = IA nên AG = \(\dfrac{2}{3}\)AD

Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).

A B C D E F I G
a) Xét \(\Delta ABC\): \(D\)là trung điểm của \(BC\), \(E\)là trung điểm của \(AC\)\(\Rightarrow\)\(ED\)là đường trung bình của \(\Delta ABC\).
\(\Rightarrow ED\)//\(AB\)và \(ED=\frac{1}{2}AB\). \(F\)là trung điểm của \(AB\)\(\Rightarrow ED=AF=FB=\frac{1}{2}AB\)
\(ED\)//\(AB\Rightarrow ED\)//\(AF\Rightarrow ID\)//\(AF\). Mà \(FI\)//\(AD\).
\(\Rightarrow FI=AD\)và \(ID=AF\)(Tính chất đoạn chắn)
Mà \(ED=AF\Rightarrow ED=ID\).
Xét \(\Delta EDB\)và \(\Delta IDC:\)
\(DB=DC\)
\(\widehat{EDB}=\widehat{IDC}\)(Đối đỉnh) \(\Rightarrow\Delta EDB=\Delta IDC\)\(\left(c.g.c\right)\)
\(ED=ID\)
\(\Rightarrow\widehat{BED}=\widehat{CID}\)(2 góc tương ứng) và 2 góc này nằm ở vị trí so le trong \(\Rightarrow IC\)//\(BE\)
Đồng thời \(IC=BE\)(2 cạnh tương ứng)
b) \(AD\)//\(FI\Rightarrow\widehat{AGE}=\widehat{FHG}\Rightarrow\widehat{FHG}=90^0\)(Đồng vị). Mà \(BE\)//\(IC\)\(\Rightarrow\widehat{FHB}=\widehat{FIC}=90^0\)(Đồng vị)
\(\Rightarrow\Delta ICF\)là tam giác vuông tại \(I\).
Ta có: \(FI=AD\),\(IC=BE\)(cmt) \(\Rightarrow FI+IC+CF=AD+BE+CF\)(đpcm)
Tham khảo:
a)
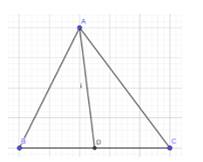
- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
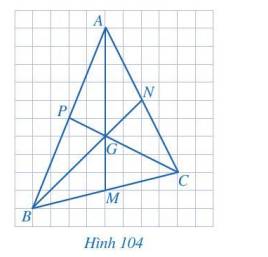
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
\(\dfrac{{BG}}{{BE}} = \dfrac{2}{3};\dfrac{{CG}}{{CF}} = \dfrac{4}{6};\dfrac{{AG}}{{AD}} = \dfrac{{4.4}}{{6.6}}\)
- Ta thấy sau khi rút gọn các tỉ số ta có :
\(\dfrac{{BG}}{{BE}} = \dfrac{{CG}}{{CF}} = \dfrac{{AG}}{{AD}} = \dfrac{2}{3}\)