Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền

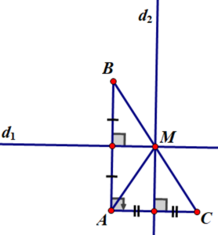
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
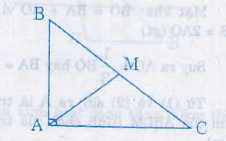
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1212 BC
Vì G là trọng tâm của ∆ ABC nên AG =2323 AM => AG =2323.1212 BC
=> AG = 1313 BC = 1313 .5 = 1.7cm

Gọi D là trung điểm BC; E là trung điểm AC
Trong tam giác ABC có BC2 = AB2 + AC2 = 32 + 42 = 25
=> BC = 5
Trong tam giác vuông ABC có AD là đường trung tuyến ứng với cạnh huyền BC nên AD = BD = CD
mà BD = CD = BC/2 = 5/2 = 2,5 nên AD = 2,5
Ta có AG/AD = 2/3 => AG = (AD.2)/3 = (2,5 x 2)/3 = 5/3

A B C M A'
a.Lấy tam giác vuong ABC bất kì, gọi AM là đường trung tuyến ứng với cạnh huyền BC
=>MB=MC=1/2BC
Trên tia đối tia MA lấy A' sao cho MA=MA'=1/2AA'
tam giác BMA và tam giác CMA': BM=MC(gt)
góc BMA= góc CMA'(đối đỉnh)
MA=MA'
=> tam giác BMA= tam giác CMA'(c.g.c)
=> BA=CA' và góc ABM = góc MCA'(2)
Từ (2) => BA//CA'
Vì BA//CA' (cmt) và BA vuông góc AC => A'C cuông góc AC
tam giác BAC và tam giác A'CA: AC chung
góc BAC = góc A'CA (= 90)
BA = A'C(cmt)
=> tam giác BAC = tam giác A'CA(c.g.c)
=>BC = A'A
=> 1/2BC = 1/2 A'A = AM (đpcm)
b. Tam giác ABC có vuông ko ?

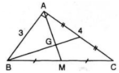
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)
⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)
Gọi M là trung điểm của BC ⇒ AM là trung tuyến.
Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên
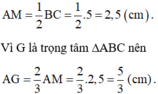
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.
Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = BC
BC
mà AM = MB nên MA = BC
BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.