Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
![]()
Ta có:

Dễ thấy tập hợp điểm biểu diễn số phức w là đường tròn tâm (5;7) bán kính 5 13

Đáp án C
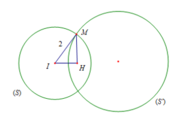
Bài giao hai mặt cầu:
Gọi M(x;y;z) theo bài M A 2 + M O → . M B → = 16
⇒ x + 2 2 + y 2 + ( z + 2 2 ) 2 + x ( x + 4 ) + y ( y + 4 ) + z 2 = 16
![]()
Giao tuyến của (S) và (S') là nghiệm của hệ phương trình:
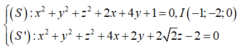
![]()

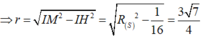

Thay toạ độ A; B vào (P) thấy ra kết quả cùng dấu, vậy A và B nằm cùng phía so với (P)
Gọi C là điểm đối xứng A qua (P) thì MA+MB nhỏ nhất khi và chỉ khi M trùng giao điểm của BC và (P)
Phương trình đường thẳng d qua A và vuông góc (P): \(\left\{{}\begin{matrix}x=2+t\\y=2t\\z=3+2t\end{matrix}\right.\)
Giao điểm D của d và (P) là nghiệm:
\(2+t+2\left(2t\right)+2\left(3+2t\right)+1=0\Rightarrow t=-1\Rightarrow D\left(1;-2;1\right)\)
\(\overrightarrow{AD}=\left(-1;-2;-2\right)\) mà \(\overrightarrow{AD}=\overrightarrow{DC}\Rightarrow C\left(0;-4;-1\right)\)
\(\overrightarrow{CB}=\left(3;3;6\right)\Rightarrow\overrightarrow{u_{BC}}=\left(1;1;2\right)\Rightarrow\) pt BC: \(\left\{{}\begin{matrix}x=3+t\\y=-1+t\\z=5+2t\end{matrix}\right.\)
Toạ độ M là nghiệm:
\(3+t+2\left(1-t\right)+2\left(5+2t\right)+1=0\Rightarrow t=-\frac{12}{7}\Rightarrow M\left(\frac{9}{7};-\frac{19}{7};\frac{11}{7}\right)\)
\(\Rightarrow T=\frac{563}{49}\)

Đáp án C.
Ta có:

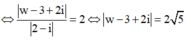
Do đó tập hợp điểm biểu diễn w là đường tròn tâm (3;-2) bán kính R= 2 5


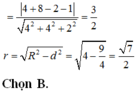



Gọi \(N\left(4;-1;-3\right)\Rightarrow2\overrightarrow{NA}-\overrightarrow{NB}=0\)
\(2MA^2-MB^2=4\)
\(\Leftrightarrow2\left(\overrightarrow{MN}+\overrightarrow{NA}\right)^2-\left(\overrightarrow{MN}+\overrightarrow{NB}\right)^2=4\)
\(\Leftrightarrow MN^2+2NA^2-NB^2+2\overrightarrow{MN}\left(2\overrightarrow{NA}-\overrightarrow{NB}\right)=4\)
\(\Leftrightarrow MN^2=4+NB^2-2NA^2=28\)
\(\Rightarrow MN=2\sqrt{7}\Rightarrow\) M thuộc mặt cầu (C) tâm N bán kính \(R=2\sqrt{7}\) có pt:
\(\left(x-4\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=28\)
Mà \(M\in\left(P\right)\Rightarrow\) quỹ tích M là đường tròn giao tuyến của mặt phẳng (P) và mặt cầu (C)
Theo định lý Pitago: \(r=\sqrt{R^2-d^2}\) với \(d\) là khoảng cách từ N tới mặt phẳng (P)
Bạn tự tính và thay số nốt đoạn còn lại.