Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

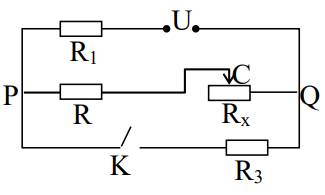
1. Khi khóa K mở, sơ đồ mạch điện như sau: R1 nt R2 nt Rx
Công suất tỏa nhiệt trên biến trở là: \(P_x=U_xI=I^2R_x=\dfrac{U^2}{\left(R_1+R_2+R_x\right)}R_x\)
\(\Leftrightarrow P_x=\dfrac{U^2}{\dfrac{R_1+R_2}{R_x}+1}\)
Để \(\left(P_x\right)_{max}\) thì \(\left(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\right)_{min}\)
Áp dụng BĐT Cosi vào hai số \(\dfrac{R_1}{R_x}\) và \(\dfrac{R_2}{R_x}\) ta có:
\(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\ge2\sqrt{\dfrac{R_1R_2}{R_x^2}}\)
Dấu "=" xảy ra khi \(\dfrac{R_1}{R_x}=\dfrac{R_2}{R_x}\)\(\Rightarrow R_2=R_1=12\Omega\)
2. Khi K đóng, sơ đồ mạch điện như sau: R1 nt [(R2 nt Rx)//R3]
Công suất tỏa nhiệt đoạn mạch PQ là: \(P=U_{23x}.I=I^2R_{23x}=\dfrac{U^2}{\left(R_1+R_{23x}\right)^2}.R_{23x}\)
\(\Leftrightarrow12=\dfrac{24^2}{\left(12+R_{23x}\right)^2}.R_{23x}\)
\(\Rightarrow R_{23x}=12\Omega\)
Ta có: \(R_{23x}=\dfrac{\left(R_2+R_x\right)R_3}{R_2+R_3+R_x}\)\(\Leftrightarrow12=\dfrac{\left(12+R_x\right).18}{12+18+R_x}\)
\(\Rightarrow R_x=24\Omega\)

a) Vì R1 nt R2 nên: Rtd = R1 + R2= 24+12= 36(ôm)
R1 nt R2 thì: I= I1= I2 = 0,5 (A)
HĐT giữa 2 đầu mỗi điện trờ là: I1=U1/R1 => U1=I1.R1 = 0,5 x 24= 12 (V)
I2=U2/R2 => U2=I2.R2= 0,5 x 12= 6(V)
b) Đổi: 20p = 1200s
Nhiệt lượng toả ra trong 20p của đoạn mạch là: Q= I2.Rtd.t= (0,5)2 . 36.1200= 10800(J)
c) Tóm tắt:
R3//R1
I2=3I1
Giải:

a) Điện trở tương đương toàn mạch :
\(R_{tđ}=R_1+\dfrac{R_2\cdot R_3}{R_2+R_3}=10+\dfrac{20\cdot60}{20+60}=10+15=25\left(\Omega\right)\)
Cường độ dòng điện qua điện trở \(R_1\):
\(I_C=I_1=\dfrac{U}{R_{tđ}}=\dfrac{12}{25}=0,48\left(A\right)\)
Hiệu điện thế 2 đầu \(R_1\)
\(U_1=I_1\cdot R_1=0,48\cdot10=4,8\left(V\right)\)
Hiệu điện thế của đoạn mạch song song :
\(U_{//}=U-U_1=12-4,8=7,2\left(V\right)\)
Cường độ dòng điện qua điện trở R2,R3 :
\(I_2=\dfrac{U_{//}}{R_2}=\dfrac{7,2}{20}=0,36\left(A\right)\)
\(I_3=\dfrac{U_{//}}{R_3}=\dfrac{7,2}{60}=0,12\left(A\right)\)
Công suất tỏa nhiệt trên toàn mạch :
\(P=UI_C=12\cdot0,48=5,76\left(W\right)\)
b) Theo đề ta có :
\(I_C'=\dfrac{U}{R_{tđ}'}\Leftrightarrow0,5=\dfrac{12}{R_X+\dfrac{R_1R_2}{R_1+R_2}}\Leftrightarrow0,5=\dfrac{12}{R_X+15}\)
Giải tìm \(R_X\) được \(R_X=9\left(\Omega\right)\)
Vậy giá trị \(R_X=9\left(\Omega\right)\).

a, Rtd=25Ω
vì R1nt(R2//R3) => I mạch=I1 =I23=U/Rtd=12/25=0.48A
=>U1=I1R1=0.48x10=4.8V =>U23=U-U1=12-4.8=7.2V
mà R3//R2 => U2=U3=U23=7.2V
=>I2=U2/R2=7.2/20=0.36 I3=0.12A
công suất tỏa nhiệt trên toàn mạch là
Ptoàn mạch=p1+p2+p3=U1I1+U2I2+U3I3=5.76W
b, Rtd=12/0.5=24Ω
ta lại có Rtd=Rx+\(\dfrac{R2.R3}{R2+R3}\)=Rx+15=>Rx=Rtd-15=24-15=9

a) Vẽ sơ đồ mạch điện và tính cường độ dòng điện qua R2 khi Rx = 45 Ω.
b) Tìm Rx khi dòng qua R3 là 0,15 A.
b) Cường độ dòng điện qua từng điện trở thay đổi thế nào khi tăng Rx còn các
điện trở khác giữ nguyên giá trị.

a)\(R_1ntR_2\Rightarrow R_{12}=R_1+R_2=15+12=27\Omega\)
\(I=\dfrac{U}{R}=\dfrac{18}{27}=\dfrac{2}{3}A\)
Công suất toả nhiệt: \(P=U\cdot I=RI^2=27\cdot\left(\dfrac{2}{3}\right)^2=12W\)
b)\(R_3//\left(R_1ntR_2\right)\Rightarrow R_{tđ}=\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}\)
\(P_{AB}=24W\Rightarrow R_{tđ}=\dfrac{U^2}{P}=\dfrac{18^2}{24}=13,5\Omega\)
\(\Rightarrow\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}=13,5\Rightarrow\dfrac{27\cdot R_3}{27+R_3}=13,5\)
\(\Rightarrow R_3=27\Omega\)

(R1 nt R2)//(R3 nt Rx)
a,\(=>Rtd=\dfrac{\left(R1+R2\right)\left(R3+Rx\right)}{R1+R2+R3+Rx}=\dfrac{\left(12+8\right)\left(16+14\right)}{12+8+16+14}=12\Omega\)
\(=>Im=\dfrac{Um}{Rtd}=\dfrac{48}{12}=4A\)
b, \(=>Ix=Ix3,,,I1=I12\)(gọi điện trở Rx là y(ôm)
theo bài ra \(=>Ix=\dfrac{1}{3}I1=>I3x=\dfrac{1}{3}I12=>I12=3I1x\)
\(=>\dfrac{U12}{R1+R2}=3.\dfrac{U3x}{R3+y}=>\dfrac{48}{12+8}=\dfrac{3.48}{16+y}=>y=44\Omega=>Rx=44\Omega\)