Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai nguồn vuông pha sẽ không có trong đề thi đâu bạn nhé
Bước sóng \(\lambda = v/f=2cm\)
A B M d1 d2 B'
Lấy B' cách B \(\dfrac{\lambda}{4}\), khi đó B' trễ pha \(\pi/2\) so với B \(\Rightarrow\) B' cùng pha với A.
Điểm M dao động biên độ cực tiểu khi
\(MB'-MA=(k+0,5)\lambda\)
\(\Rightarrow d_2-\dfrac{\lambda}{4}-d_1=(k+0,5)\lambda\)
\(\Rightarrow d_2-d_1=(k+0,75)\lambda\)
\(-12\le d_2-d_1\le12\)
\(\Rightarrow -12\le (k+0,75).2\le12\)
\(\Rightarrow -6,74\le k \le5,25\)
Bạn xét k = -6 hoặc k = 5 để tìm \(d_1, d_2\), lấy giá trị d nhỏ nhất, từ đó suy ra khoảng cách lớn nhất.

Điểm A sớm pha hơn B là: \(\frac{2}{3}\pi\)
Điểm M dao động với biên cực đại khi: \(d_2-\left(d_1-\frac{\lambda}{3}\right)=k\lambda\Rightarrow d_2-d_1=k\lambda-\frac{\lambda}{3}\)
Giả sử M lệch phía A, cách trung điểm AB là x thì:\(d_2-d_1=\frac{AB}{2}+x-\left(\frac{AB}{2}-x\right)=2x=k\lambda-\frac{\lambda}{3}\)
\(\Rightarrow x=\frac{k\lambda}{2}-\frac{\lambda}{6}\)
Nhận thấy xmin khi k = 0 \(\Rightarrow x_{min}=-\frac{\lambda}{6}\)
Dấu "-" chứng tỏ x lệch về phía ngược lại mà tả đã giả sử, là phía B.

Với bài toán này, bạn chỉ cần tìm những điểm dao động với biên độ 5mm trên đoạn AB, rồi x2 lên.
A B M d1 d2
Bước sóng: \(\lambda=1,5cm\)
Do biên độ của M là 5mm, nên sóng do A và B truyền đến M vuông pha nhau (\(3^2+4^2=5^2\))
Suy ra: \(d_2-d_1=\left(k+0,5\right)\frac{\lambda}{2}\)
\(-10\le d_2-d_1\le10\Leftrightarrow-10\le\left(k+0,5\right)\frac{\lambda}{2}\le10\Leftrightarrow-10\le\left(k+0,5\right)\frac{1,5}{2}\le10\Leftrightarrow-13,83\le k\le12,83\)
Suy ra: k = -13;-12,....; 11;12
Có 26 điểm thỏa mãn.
Như vậy có 26x2 = 52 điểm dao động với biên độ 5cm trên parabol.

Điểm B sớm pha hơn A.
Để M dao động với biên cực đại thì: \(\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\Rightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)
Kể từ trung trực AB, đường cực đại thứ 1 khi k = 0
Đường thứ 2 khi k = 1
M thuộc đường thứ 3 khi k =2 \(\Rightarrow2\lambda+\frac{\lambda}{6}=24-11=13\Rightarrow\lambda=6cm\)
Vận tốc: \(v=\lambda f=6.50=300\) (cm/s)
@phynit : lần trước bạn có giải thích cho mình giả sử B' cùng pha vs A suy ra B' trễ pha hơn B là pi/3
vậy từ pi/3 ra lamđa/6 kiểu gì bạn?

S1 S2 I M x
Giả sử S1S2 = 2d, điểm M cách trung điểm I một đoạn x có biên độ 1cm.
Bước sóng: \(\lambda=\frac{v}{f}=\frac{40}{20}=2cm\)
Giả sử sóng do S1 đến M lệch pha hơn sóng do S2 đến M là \(\varphi\), ta có: \(\varphi=\frac{4\pi x}{\lambda}\)
Biên độ của M là tổng hợp 2 dao động do S1 và S2 đến, ta có: \(6^2+8^2+2.6.8.\cos\varphi=1\Rightarrow\cos\varphi=\frac{-99}{96}<-1\), vô lí
Bạn xem lại xem đề bài có nhầm lẫn đâu không nhé.
Bạn làm sai rồi nhé, kia là mm và cm, đề này chuẩn
Đáp án 0,25 nhé baby ![]()

Giữa M và trung trực của AB có 2 cực đại khác nên M là cực đại thứ 3 kể từ trung trực.
Vì: \(d_1-d_2=\text{k}\lambda-\frac{\lambda}{6}\)
Nên: k = 1 là cực đại thứ 1 (để cho d1 - d2 > 0).
k = 2 là cực đại thứ 2.
M là cực đại thứ 3 nên k = 3 bạn nhé.

Điểm M dao động với biên độ cực đại thì: \(MA-\left(MB-\frac{\Delta\varphi}{2\pi}\lambda\right)=k\lambda\)
\(\Rightarrow MA-MB=k\lambda-\frac{\Delta\varphi}{2\pi}\lambda\)
Thay \(\Delta\varphi=-\frac{\pi}{3}\) vào biểu thức trên thì: \(\Rightarrow MA-MB=k\lambda-\frac{\lambda}{6}=\frac{\lambda}{3}\)(giả thiết)
Không tìm đc giá trị nguyên k thỏa mãn PT trên, nên \(\Delta\varphi=-\frac{\pi}{3}\) không thỏa mãn.
bạn ơi đấy là đáp án D trong ABCD
A. -pi/6 b. -2pi/3 c.2pi/3 d. -pi/3
cả A và B đều không thỏa mãn giống D mà

- Từ phương trình của 2 nguồn ta thấy sóng của 2 nguồn vuông pha nhau thì số cực đại và cực tiểu là như nhau và:
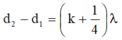
- Giữa M và đường trung trực AB còn có 2 dãy cực đại và tại M là cực tiểu → k = 2
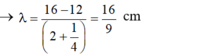
- Tốc độ truyền sóng là:
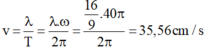

B sớm pha hơn A nên điểm M dao động với biên độ cực đại thì:
\(\left(d_1-\frac{\lambda}{6}\right)-d_2=k\lambda\Leftrightarrow d_1-d_2=k\lambda+\frac{\lambda}{6}\)(*)
A B M d1 d2
Bước sóng: \(\lambda=2cm\)
M cách A lớn nhât thì d1 phải lớn nhất thỏa mãn (*)
\(d_1-d_2\le10\Rightarrow k\lambda+\frac{\lambda}{6}\le10\Rightarrow k.2+\frac{2}{6}\le10\Rightarrow k\le4,83\)
k nguyên \(\Rightarrow k=4\)
Ta có hệ:
\(\begin{cases}d_1-d_2=4\cdot2+\frac{2}{6}=\frac{25}{3}\\d_1+d_2=10\end{cases}\)
suy ra: \(d_1=\left(\frac{25}{3}+10\right):2=9,17cm\)
Đáp án là câu D. Chúc các bạn làm bài tốt