Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2=3[\left(x^4+2x^2+1\right)-x^2]-\left(x^2+x+1\right)^2\)\(=3[\left(x^2+1\right)^2-x^2]-\left(x^2+x+1\right)^2\)
\(=3\left(x^2-x+1\right)\left(x^2+x+1\right)-\left(x^2+x+1\right)^2\)
\(=\left(x^2+x+1\right)\left(2x^2-4x+2\right)=2\left(x-1\right)^2\left(x^2+x+1\right)\)

bài 1:vì x^3 + ax + b chia hết cho (x-1)^2 nên khi nhóm nhân tử chung lại thì x^3 + ax + b có dạng:
(x-1)^2(mx + n)
nhân phá ra bạn sẽ có(x^2 -2x + 1)(mx + n) = m.x^3 + n.x^2 - 2m.x^2 - 2n.x + m.x + n
= m.x^3 + x^2 (n -2m) + x(m -2n) + n
vì nó có dạng x^3 + ax + b nên ta sẽ có: m = 1
và n -2m = 0
hay n -2 = 0
hay n =2.
suy ra đa thức sẽ bằng:
x^3 -3x + 2
từ đó suy ra a = -3 và b = 2.
bài 2:bạn nhận thấy : n^3 + 3n^2 - n - 3 = n^2(n+3) - (n+3) = (n-1)(n+1)(n+3)
vì n lẻ => n -1 là số chẵn
n +1 là số chẵn
n + 3 là số chẵn
đặt n-1 = a ( a chẵn) suy ra ta có:
a(a +2)(a+4)
bạn thấy a(a +2)(a+4) là tích 3 số chẵn liên tiếp nên chia hết cho 48 (bạn có thể tự biện luận từ số 48 = 2.4.6 là tích 3 số chẵn liên tiếp nhỏ nhất không chứa 0 nên suy ra tích 3 số chẵn liên tiếp luôn chia hết cho 48)
suy ra a(a+2)(a+4) chia hết cho 48.
suy ra (n-1)(n+1)(n+3) chia hết cho 48
suy ra n^3 + 3n^2 - n - 3 luôn chia hết cho 48 với n lẻ (đpcm)

a)\(f\left(x\right)=x^4+2x^3-x-2\)
\(=x^4+2x^3+x^2-x^2-x-2\)
\(=\left(x^2+x\right)^2-\left(x^2+x\right)-2\)
Đặt \(x^2+x=t\) ta có:
\(=t^2-t-2\)\(=\left(t-2\right)\left(t+1\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+1\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+1\right)\)


\(\left(x+1\right)^4+\left(x^2+x+1\right)^2\)
\(=\left(x+1\right)^4+x^2\cdot\left(x+1\right)^2+2x\left(x+1\right)+1\)
\(=\left(x+1\right)^2\cdot\left[\left(x+1\right)^2+x^2\right]+2x^2+2x+1\)
\(=\left(2x^2+2x+1\right)\left(x^2+2x+1+1\right)\)
\(=\left(2x^2+2x+1\right)\left(x^2+2x+2\right)\)
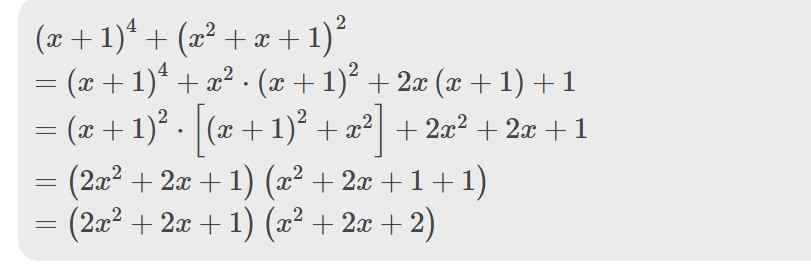
theo đề bài ta có: (x-1)^2=x^2-2x+1
ta lại có x^3:x^2=x
do đó thương của phép chia đã cho là x+m
(x^3+ax+b) chia hết cho x^2-2x+1
<=> x^3+ax+b=(x^2-2x+1)(x+m)
<=> x^3+ax+b=x^3+x^2m-2x^2-2xm+x+m
<=> x^3+ax+b=x^3+(m-2)x^2+(-2m+1)x+m
Đồng nhất 2 vế ta được :m-2=0=>m=2
-2m+1=a =>-2.2+1=-3=>a=-3
b=m=>b=2