Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/. Xét Tứ giác AEHF, có:
E = 90 (EH vuong góc AB)
F = 90 (HF vuong AC)
A = 90 (ABC vuong tai A)
=> AEHF là hcn
2/. Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM =1/2BC => AM =MB = MC = 2,5 cm
=> BC = 2,5 x2 = 5cm
Áp dụng định lý Py-ta-go vào tam giác vuông ABC, có:
AB^2 +AC^2 =BC^2
9+AC^2 = 25
=> AC^2 = 25-9 = 16
=> AC =4cm
Diện tích tam giác ABC: 1/2AB.AC = 1/2(.3.4 )= 6cm^2
3/. Gọi K là giao điểm của EF và AM, J là giao điểm của EF và AH
CM: góc AEK = góc ABC
Vì J là giao điểm của 2 đường chéo trong hcn AEHF => ẠJ = JH = Ẹ = JF
=> tam giác EJA cân tại J => AEJ = EAH (1)
Xét tam giác vuông ABH => EAH +ABC = 90
Xét tam giác vuông ABC=> ABC + ACB = 90
=> EAH = ACB và (1) => ACB = AEJ (2)
Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM = BM = MC
=> tam giác ABM cân tại M => EAK = ABC (3)
Xét tam giác EAK: có: AEJ + EAK = ACB + ABC = 90 ( do 2 và 3)
=> tam giác AEK vuong tại K
Hay AM vuông EF
4/. Vì A đới xứng với I qua BC => AI vuông góc với BC . Mà AH vuong với BC => A. H , I thẳng hàng . hay H là trung điểm của AI
Xét tam giác AID, có:
H là trung ddierm của AI, M là trung điểm của AD
=> HM là đường trung bình của tam giác AID => HM // ID
=> tứ giác BIDC là hình thang
Xét tam giác ABI , có: BH vừa là đường cao vừa là đường trung tuyến => ABI cân tại B => IBH = ABH (BH là đường phân giác) (4)
Xét tứ giác ABCD có:
M là trung điểm BC
M là trung điểm AD
M = BC giao AD
=> ABCD là hình bình hành và A = 90 => ABCD là hình chữ nhật
=> DCB = ABC (DC // AB và solle trong) (5)
Từ 4 và 5 => BCD = IBC (= ABC) => Hình thang BIDC là hình thang cân
1/. Xét Tứ giác AEHF, có:
E = 90 (EH vuong góc AB)
F = 90 (HF vuong AC)
A = 90 (ABC vuong tai A)
=> AEHF là hcn
2/. Vì AM là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC => AM =1/2BC => AM =MB = MC = 2,5 cm
=> BC = 2,5 x2 = 5cm
Áp dụng định lý Py-ta-go vào tam giác vuông ABC, có:
AB^2 +AC^2 =BC^2
9+AC^2 = 25
=> AC^2 = 25-9 = 16
=> AC =4cm
Diện tích tam giác ABC: 1/2AB.AC = 1/2(.3.4 )= 6cm^2
3/.

1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
2: AM=2,5cm nên BC=5cm
=>AC=4cm
S=3x4/2=6cm2
3:
Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AFE=góc AHE=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc ACB
=>góc MAC+góc EFA=90 độ
=>AM vuông góc với EF
4:
Xét ΔADI có
H,M lần lượt là trung điểm của AI và AD
nên HM là đường trung bình
=>HM//DI
=>DI//BC
Xét ΔCIA có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCIA cân tại C
=>CI=CA=DB
=>BIDC là hình thang cân

a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành

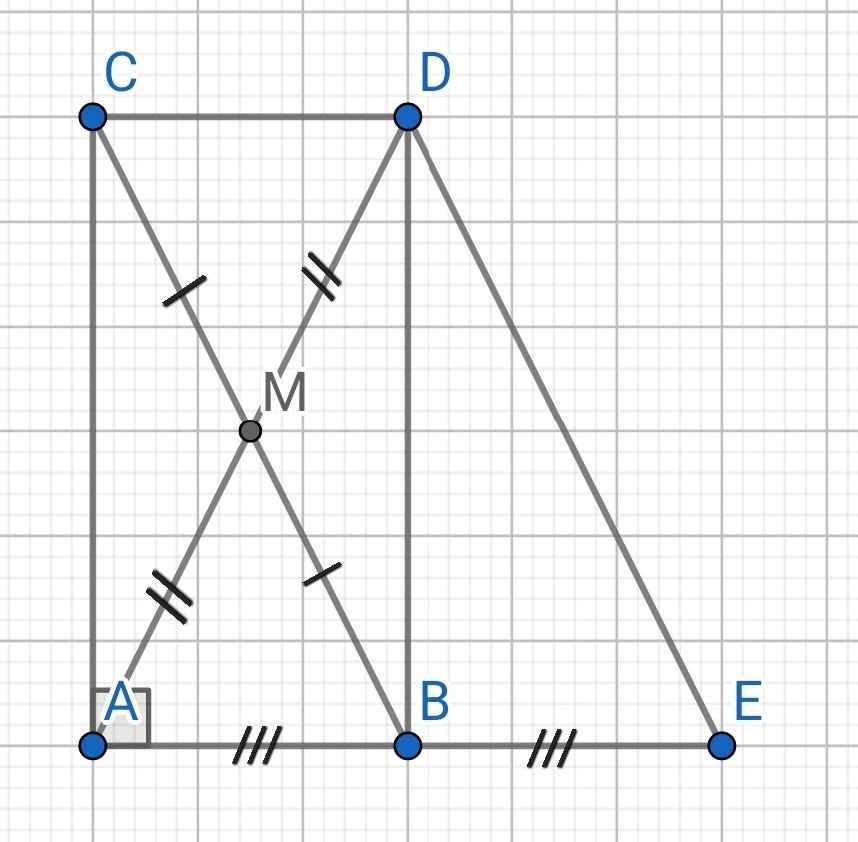 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật

b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
b,d: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AFE=góc AHE=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc ACB
=>góc MAC+góc EFA=90 độ
=>AM vuông góc với EF
c: Xét ΔADI có
H,M lần lượt là trung điểm của AI và AD
nên HM là đường trung bình
=>HM//DI
=>DI//BC
Xét ΔCIA có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCIA cân tại C
=>CI=CA=DB
=>BIDC là hình thang cân