Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với dạng bài toán này thì ta có thể giải theo 2 cách:
Cách 1:
Áp dụng công thức:
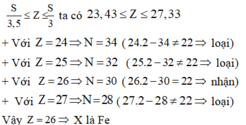
Cách 2: Gọi số p, n, e trong nguyên tử lần lượt là Z, N, E (nguyên dương)
+ Nguyên tử của nguyên tố X có tổng số hạt cơ bản (proton, nơtron, electron) là 82 hạt: 2Z + N = 82
+ Hạt mang điện nhiều hơn hạt không mang điện là 22 hạt: 2Z - N = 22
Từ đó ta có:
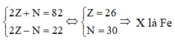
Đáp án A.

Ta có: \(\left\{{}\begin{matrix}p+e+n=58\\p=e\\p+e-n=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=40\\2p+n=58\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=19\\n=20\end{matrix}\right.\)

a) Ta có: \(\left\{{}\begin{matrix}p+e+n=155\\p=e\\p+e-n=33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=47\\n=61\end{matrix}\right.\)
\(\Rightarrow A=p+n=47+61=108\left(u\right)\)
\(KHNT:^{108}_{47}Ag\)
b)
Ta có: \(\left\{{}\begin{matrix}p+e+n=95\\p=e\\\dfrac{p+n}{e}=\dfrac{13}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=30\\n=35\end{matrix}\right.\)
\(\Rightarrow A=p+n=30+35=65\left(u\right)\)
\(KHNT:^{65}_{30}Zn\)
c)
Ta có: \(\left\{{}\begin{matrix}p+n=80\\p=e\\n-p=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=35\\n=45\end{matrix}\right.\)
\(\Rightarrow A=p+n=35+45=80\left(u\right)\)
\(KHNT:^{80}_{35}Br\)
d)
Ta có: \(\left\{{}\begin{matrix}p+e+n=52\\p=e\\n-e=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=17\\n=18\end{matrix}\right.\)
\(\Rightarrow A=p+n=17+18=35\left(u\right)\)
\(KHNT:^{35}_{17}Cl\)

a) \(\left\{{}\begin{matrix}2Z+N=52\\2Z-N=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}Z=17\\N=18\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}2Z+N=95\\2Z-N=25\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}Z=30\\N=35\end{matrix}\right.\)
