
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng

\(I=\int e^xcosxdx\Rightarrow\left\{{}\begin{matrix}u=cosx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-sinx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=e^xcosx+\int e^xsinx.dx=e^xcosx+I_1\)
\(I_1=\int e^xsinx\Rightarrow\left\{{}\begin{matrix}u=sinx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=cosx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I_1=e^xsinx-\int e^xcosx.dx=e^x.sinx-I\)
\(\Rightarrow I=e^xcosx+e^xsinx-I\Rightarrow2I=e^x\left(cosx+sinx\right)\)
\(\Rightarrow I=e^x\left(\frac{1}{2}cosx+\frac{1}{2}sinx\right)+C\Rightarrow\left\{{}\begin{matrix}A=\frac{1}{2}\\B=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow A+B=1\)

đầu bài có vấn đề cmnr vs y=-x^3+3mx+1 =>y'=-3x^2+3m => x=+-can(m) vs x=-can(m)=> y=-(can(m))^3+3m(-can(m)+1 =-4can(m)^3+1 vs x=can(m) =>y=4can(m)^3+1 . đặt can(m)=a => điểm A(-a;-4a^3+1) B(a;4a^3+1) vì tạo tam giác vuông nên tích vecto OA*OB=0 => -a^2 +(1+4^3a)(1-4a^3)=0<=>-a^2 +1- 16a^6 =0đặt a^2=b => -16b^3-b+1=0 => b=1/4( nhận) b=-1/4 ( loại)=> x^2=1/4 mà can(m)=x =>m=x^2 =1/4 kq là 1/4 nên k có kq nếu đầu bài là y=-x^3+3m^2x+1 thì ra 1/2. k biết mk sai hay đề sai nữa

\(y'=4x\left(x-m\right)\left(x+m\right)\\ y'=0\Leftrightarrow\begin{cases}x=0\\x=\pm m\end{cases}\)
Với m=0 thì hàm số có 3 cực trị là 0, -m và m
đồ thị hàm số có 3 điểm cực trị \(A\left(0;1\right),M\left(-m;1-m^4\right),N\left(m;1-m^4\right)\)
Nhận thấy \(AM=AN\) nên \(\Delta AMN\) cân tại A với mọi m
Gọi trung điểm MN là \(I\left(0;1-m^4\right)\)
\(\Delta AMN\) vuông cân tại A khi và chỉ khi \(IA=IM=IN\) hay\(IA=IN\)
\(\Leftrightarrow IA=IN\Leftrightarrow\left|m^4\right|=\left|m\right|\Leftrightarrow m=\pm1\) (vì \(m\ne0\))

1)
Dễ thấy \(f(x)=\sqrt{2}-\sqrt{x-1}\leq \sqrt{2}\) nên chỉ cần $0<k<\sqrt{2}$ là bất phương trình có nghiệm
2)
Xét \(y=\sqrt{x^2-1}+\sqrt{x+1}; y'=0\Leftrightarrow x=-1\)
Do đó $y_{min}=0$, hàm số không tồn tại max. Với đk $m$ để phương trình có nghiệm thì chỉ cần $m\geq 0$ (PT luôn có nghiệm khi $m$ nằm trong khoảng max, min)

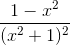 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.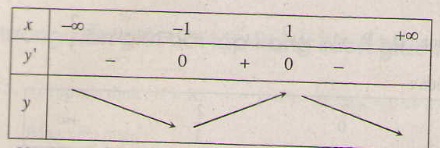
1+1=2 2+1=3
1+1=2
2+1=3