Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc điểm D kia là C?
\(\overrightarrow{AB}=\left(4;14\right)=2\left(2;7\right)\)
\(\Rightarrow\) Đường thẳng AB nhận \(\left(7;-2\right)\) là 1 vtpt
Phương trình AB:
\(7\left(x-2\right)-2\left(y-1\right)=0\Leftrightarrow7x-2y-12=0\)
\(\overrightarrow{CB}=\left(2;6\right)=2\left(1;3\right)\Rightarrow\) đường cao AH vuông góc BC nên nhận (1;3) là 1 vtpt
Phương trình AH:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)
\(\overrightarrow{AC}=\left(2;8\right)=2\left(1;4\right)\Rightarrow\) đường thẳng AC nhận (4;-1) là 1 vtpt
Phương trình AC: \(4\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow4x-y-7=0\)
Gọi \(M\left(x;y\right)\) là điểm bất kì thuộc phân giác góc A
\(\Rightarrow d\left(M;AB\right)=d\left(M;AC\right)\)
\(\Rightarrow\dfrac{\left|7x-2y-12\right|}{\sqrt{7^2+\left(-2\right)^2}}=\dfrac{\left|4x-y-7\right|}{\sqrt{4^2+\left(-1\right)^2}}\)
\(\Leftrightarrow\sqrt{17}\left|7x-2y-12\right|=\sqrt{53}\left|4x-y-7\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}7\sqrt{17}x-2\sqrt{17}y-12\sqrt{17}=4\sqrt{53}x-\sqrt{53}y-7\sqrt{53}\\7\sqrt{17}x-2\sqrt{17}y-12\sqrt{17}=-4\sqrt{53}x+\sqrt{53}y+7\sqrt{53}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(7\sqrt{17}-4\sqrt{53}\right)x+\left(\sqrt{53}-2\sqrt{17}\right)y-12\sqrt{17}+7\sqrt{53}=0\\\left(7\sqrt{17}+4\sqrt{53}\right)x-\left(\sqrt{53}+2\sqrt{17}\right)y-12\sqrt{17}-7\sqrt{53}=0\end{matrix}\right.\)
Đây là pt 2 phân giác trong và ngoài của góc A

Đáp án A
Ta có 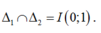
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
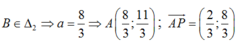
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0

Câu 1: ko dịch được đề :)
Câu 2:
Gọi d' là đường thẳng qua A và vuông góc d
\(\Rightarrow\) d' nhận \(\left(3;2\right)\) là 1 vtpt
Phương trình d': \(3\left(x-1\right)+2\left(y-2\right)=0\Leftrightarrow3x+2y-7=0\)
Câu 3:
\(\overrightarrow{CB}=\left(5;-2\right)\)
Đường thẳng AH vuông góc BC nên nhận \(\left(5;-2\right)\) là 1 vtpt
Phương trình AH:
\(5\left(x-2\right)-2\left(y+2\right)=0\Leftrightarrow5x-2y-14=0\)

b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
