Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt
\(p_1=2,02.10^6N\)/\(m^2\)
\(p_2=0,89.10^6N\)/\(m^2\)
\(d=10300N\)/\(m^3\)
________________
\(h_1=?\)
\(h_2=?\)
Giải
Dựa vào công thức tính áp suất chất lỏng: \(p=d.h\Rightarrow h=\frac{p}{d}\)
=> Độ sâu của tàu ngầm ở thời điểm áp suất là \(2,02.10^6\): \(h_1=\frac{2,02.10^6}{10,3.1^4}=\frac{p_1}{d}\approx196,1\left(m\right)\)
Độ sâu của tàu ngầm ở thời điểm áp suất là \(0,89.10^6\) là: \(h_2==\frac{p_2}{d}=\frac{0,89.10^6}{10,3.10^4}\approx86,4\left(m\right)\)

TÓM TẮT :
P = 0,86.106 N/m2
1) d = 10300N/m3
______________________________________
1) h = ?
2) Nếu tàu lặn càng sâu thì P có thay đổi không?Vì sao?
BÀI GIẢI:
1 ) Theo công thức: P = d . h
Ta có: 0,86 . 106 = 10300 . h
<=> h = 0, 86 . 106 : 10300
<=> h ≈ 83 , 5 ( m)
Vậy tàu ngầm ở độ sâu là 83 , 5 m
2) Nếu tàu lặn càng sâu thì áp suất thay đổi vì khi lặn càng sâu thì áp suất càng tăng.
KO BIẾT CÓ SAI KO ![]()
2) Nếu tàu lặn càng sâu thì áp suất đó có thay đổi ko ? Vì sao ?

a. ta thấy: \(p'>p\left(25,3\cdot10^5>15\cdot10^5\right)=>\) tàu đang lặn xuống vì càng xuống sâu áp suất càng tăng.
b. \(\left\{{}\begin{matrix}h=\dfrac{p}{d}=\dfrac{15\cdot10^5}{10300}\approx145,6\left(m\right)\\h'=\dfrac{p'}{d}=\dfrac{25,3\cdot10^5}{10300}\approx245,3\left(m\right)\end{matrix}\right.\)
a) Áp suất tác dụng lên vỏ tàu ngầm, tức là cột nước ở phía trên tàu ngầm tăng. Vậy tàu ngầm đã chìm xuống.

a) Ta có: p 1 > p 2 ( d o 2020000 > 860000 ) ⇔ d h 1 > d h 2 ⇔ h 1 > h 2 b) Tàu ngầm đang ngoi lên

a) Tàu nổi lên do áp suất lúc đầu lớn hơn lúc sau \(p_1>p_2\left(2,02.10^2< 0,86.10^2\right)\)
b) Độ sâu của tàu ở hai thời điểm trên:
\(p_1=d.h_1\rightarrow h_1=\dfrac{p_1}{d}=\dfrac{2,02.10^2}{10300}\approx0,02\left(m\right)\\ p_2=d.h_2\rightarrow h_2=\dfrac{p_2}{d}=\dfrac{0,86.10^2}{10300}\approx0,008\left(m\right)\)

a, Tàu đàn nổi lên vì áp suất sau nhỏ hơn áp suất trước, chứng tỏ độ chênh lệch độ sâu với mặt nước biển đang giảm
b, Độ sâu của tàu ở hai thời điểm:
\(h_1=\dfrac{p_1}{d}=\dfrac{2,02.10^6}{10300}=196,11(m)\)
\(h_2=\dfrac{p_2}{d}=\dfrac{0,86.10^6}{10300}=83,5(m)\)
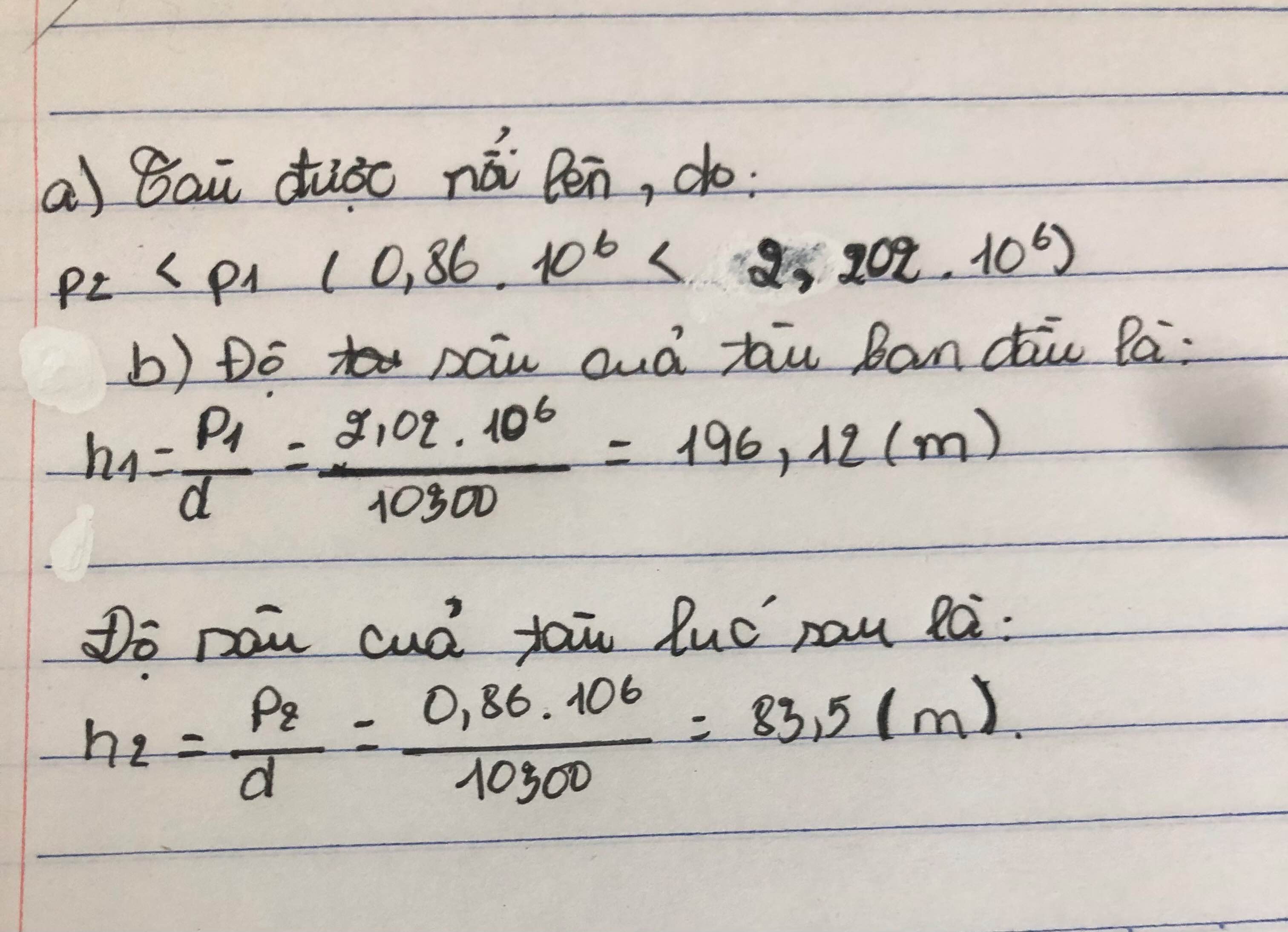
Giải
a) Áp suất tác dụng lên vỏ tàu ngầm giảm, tức cột nước ở phía trên tàu ngầm giảm. Điều này chứng tỏ tàu ngầm đã nổi lên.
b) Áp dụng công thức p=d.h; h1=\(\dfrac{p}{d}\)
Độ sâu của tàu ngầm ở thời điểm trước:
h1=\(\dfrac{p_1}{d}=\dfrac{\text{2020000}}{\text{10300}}\text{≈ 196 m }\)
Độ sâu của tàu ngầm ở thời điểm sau:
h2=\(\dfrac{p_2}{d}=\dfrac{\text{860000}}{\text{10300 }}\text{≈ 83,5m}\)