Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Diện tích da phủ kín quả bóng là:
$\4\pi r^2=\pi d^2=24^2\pi = 576\pi$ (cm2)
Diện tích da dùng để khâu bóng:
$576\pi (1+0,02)=587,52\pi$ (cm2)
Từ công thức \(S_{cầu}=4\pi r^2=1256\left(cm^2\right)\)
\(\Rightarrow r^2=\dfrac{1256}{4\pi}\approx100\left(cm\right)\Rightarrow r\approx10\left(cm\right)\)
trả lời
bài này e chưa học đến
nhưng
c có thể vào học 24 hỏi nha
chúc c học tốt
Gọi x là số múi da màu đen , y là số múi da màu trắng \((x,y\inℕ^∗)\)
Bán kính trái bóng : R = 22,3 : 2 = 11,15cm
Diện tích bề mặt trái bóng S= \(4^{\pi}\cdot R^2=1562,3cm^2\)
Ta có hpt : \(\hept{\begin{cases}x+y=32\\37\cdot x+55,9\cdot y=1562,3\end{cases}}\Rightarrow\hept{\begin{cases}x=12\\y=20\end{cases}}\)
Vậy trái bóng có 12 múi da màu đen và 20 múi da màu trắng
Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3
| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nit | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7mm | 7,32cm | 6,5cm | 40mm | 61mm |
| Độ dài đường tròn lớn | 134,08mm | 23cm | 20,41cm | 125,6mm | 171,71mm |
| Diện tích | 57,25cm2 | 168,25cm2 | 132,67cm2 | 5024mm2 | 11683,94mm2 |
| Thể tích | 40,74cm3 | 205,26cm3 | 143,72cm3 | 33,49 cm3 | 118,79cm3 |
Cách tính:
+ Quả bóng gôn:
d = 42,7mm ⇒ R = d/2 = 21,35 mm
⇒ Độ dài đường tròn lớn: C = 2π.R=2.3,14.21,35 ≈ 134,08 (mm)
⇒ Diện tích mặt cầu: S = πd2 = 3,14.(42,7)2 ≈ 5725 mm2 = 57,25 (cm2).
⇒ Thể tích khối cầu: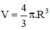 
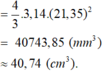
+ Quả khúc côn cầu:
C = πd = 23cm ⇒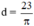 
≈ 7,32 (cm)
⇒ Diện tích mặt cầu: S = πd2=3,14.(7,32)2 = 168,25 (cm2).
⇒ Thể tích khối cầu: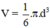 
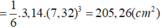
+ Quả ten-nít:
d = 6,5cm
⇒ Độ dài đường tròn lớn: C = π.d = 3,14.6,5 = 20,41 (cm)
⇒ Diện tích mặt cầu: S = πd2= 3,14.(6,5)2=132,67 (cm2)
⇒ Thể tích khối cầu: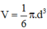 
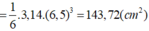
+ Quả bóng bàn:
d = 40mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.40 ≈ 125,6 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.402 = 5024 (mm2)
⇒ Thể tích khối cầu: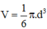 
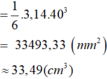
+ Quả bi-a;
d = 61mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.61 = 191,54 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.612 ≈ 11683,94 (mm2)
⇒ Thể tích khối cầu: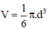 
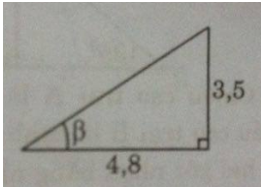
Chiều cao cột cờ là cạnh đối diên với góc giữa tia sang mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.
\(\tan B=\dfrac{35}{48}\)nên \(\widehat{B}=36^06'\)
a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:
Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
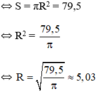
Áp dụng công thức tính thể tích hình cầu, ta có:
\(V_{cầu}=\dfrac{4}{3}\pi R^3\)
Mà thể tích hình cầu này là 288dm3 nên ta có \(\dfrac{4}{3}\pi R^3=288\Leftrightarrow\pi R^3=216\Leftrightarrow R^3=\dfrac{216}{\pi}\Leftrightarrow R=\sqrt[3]{\dfrac{216}{\pi}}=\dfrac{6}{\sqrt[3]{\pi}}\left(dm\right)\)
Áp dụng công thức tính diện tích mặt cầu, ta có \(S_{mc}=4\pi R^2=4\pi\left(\dfrac{6}{\sqrt[3]{\pi}}\right)^2=4\pi.\dfrac{36}{\sqrt[3]{\pi^2}}=144.\sqrt[3]{\pi}\approx210,9\left(dm^2\right)\)
Vậy diện tích da để làm nên quả bóng đó là khoảng 210,9dm2.