Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat{ATM}=\frac{1}{2}Sđ\widebat{AT}\),
\(\widehat{ABT}=\frac{1}{2}Sđ\widebat{AT}\).
=> \(\widehat{ATM}=\widehat{ABT}\).
b) \(\Delta MAT\)và \(\Delta MTB\)có góc M chung, góc MTA = góc MBT ( theo câu a).
Do đó \(\Delta MAT\)đồng dạng với \(\Delta MTB\)(g-g), ta có:
\(\frac{MA}{MT}=\frac{MT}{MB}\)=> MT2 = MA.MB.
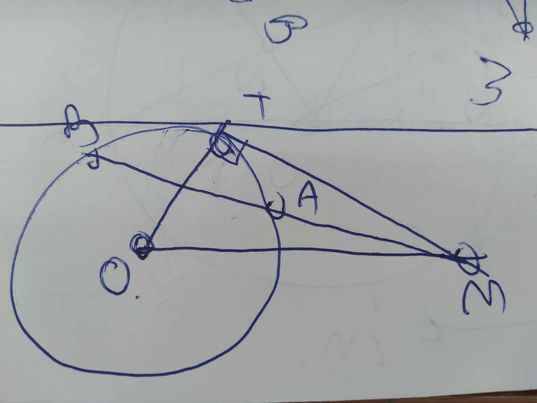
T M A O B
B, Xét tam giác
MAT và MTB có:
tam giác MTA=\(\widehat{MBT}\)
⇒△MAT∼△MTB(g.g)
⇒MAMT=MTMB⇔MT2=MA.MB (đpcm)

bài này dễ mà bạn
có MTA=1/2 sd AT
ABT=1/2 sd AT
\(\Rightarrow\)MTA=MTB
xét tam giác MTA và MBT
M chung
MTA=MTB
tam giác MTA dong dang MBT
\(\Rightarrow\)MT/AB=MA/MT\(\Rightarrow\)MT2=MA.MT

1234 m ngu k bt trả lời thì thôi đừng ở đó xàm xàm trên trang của t này câm k đừng trách t nhắn với pm với admin xóa cái acc của m!
Mất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcMất nick đau lòng con quốc quốcvMất nick đau lòng con quốc quốc

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
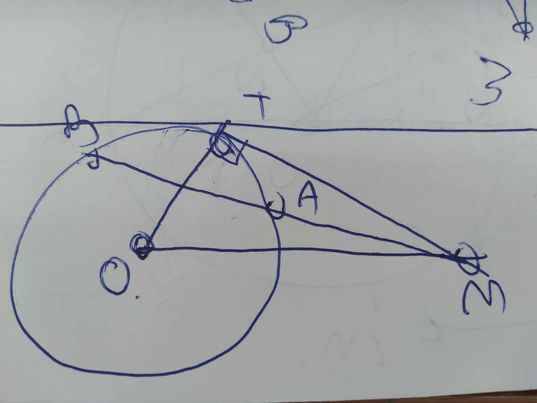

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)