Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

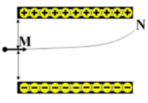
Chọn gốc tọa độ O tại vị trí electron bắt đầu vào vùng điện trường, hệ tọa độ xoy có dạng như hình vẽ:
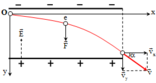
Thành phần Ox chuyển động thẳng đều: x = v 0 t
Thành phần Oy chuyển động nhanh dần đều: y = 1 2 a y t 2
Vậy phương trình quỹ đạo của elctron là: y = 1 2 a y x v 0 2
Lực điện trường tác dụng lên electron: F → = q E → = m a → → F x = m a x = 0 F y = m a y = F
a x = 0 a y = F m = q E m = q U m d → x = v 0 t = 2.10 7 t y = 1 2 a y x v 0 2 = 1 2 q U m d v 0 2 x 2 = 2 x 2
a. Vậy phương trình quỹ đạo có dạng: y = 1 2 a y x v 0 2 = 1 2 q U m d v 0 2 x 2 = 2 x 2
b. Tính quãng đường electron đi được theo phương Ox khi nó ra khỏi tụ.
Dựa theo thành phần nằm ngang Ox ta có: x = l = 5.10 − 2 m
c. Vận tốc electron khi rời khỏi tụ:
v x = v 0 v y = v 0 y + a y t → x = v 0 t → t = x v 0 v x = 2.10 7 v y = 0 + q U m d x v 0 = 0 , 4.10 7 → v = v x 2 + v y 2 = 2.10 7
d. Công của lực điện trường khi electron bay trong tụ.
Khi electron bay ra khỏi tụ thì nó đã đi được quãng đường theo phương Oy là: y = 2 x 2
→ x = l = 5.10 − 2 m y = 2 x 2 = 50.10 − 4 m = 5 m m
Công của lực điện trường: A = F . d . c o s F → , d → ⏟ y = F . y → A = q E y = q U d y = 7 , 28.10 − 18


Từ (*) và (**) suy ra hiệu điện thế giữa hai bản: U = 2 m h v 2 e s 2 = 200 V
Vậy hiệu điện thế giữa hai bản là U = 200V.

+ Gia tốc chuyển động của electron
a = F m = e E m = e U m d ⇒ U = a m d e
+ Mặc khác
h = 1 2 a t 2 ⇒ a = 2 h t 2 = 2 h s v 2 = 2 h v 2 s 2
+ Từ hai biểu thức trên ta thu được
U = 2 m h v 2 e s 2 = 200 V