
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D
Ta có :
\(AD^2+CD^2=AC^2\) ( định lí Py - ta - go )
\(\Rightarrow2CD^2+49-14CD=169\)
\(2CD\left(CD-7\right)=120\)
\(CD\left(CD-7\right)=60\)
\(\Rightarrow S_{ABCD}=60\)

đặt chiều rộng HCN là x=>chiều dài là x+7
theo Pi-ta-go x^2+(x+7)^2=13^2 =>x^2+7x-60=0 =>chọn nghiệm dương x=5
Suy ra S hình chữ nhật=5*(5+7)=60m2
Bài làm : gọi x là chiều dài của HCN —» chiều rộng HCN = x - 7
Theo Định lý pitago ta có :
13² = (x - 7 )² + x²
<=> 169 = x² - 14x + 49 + x²
<=> 120 = 2x² - 14x
<=> 2x² - 14x - 120 = 0
bấm máy dc : x= -5 ( loại khoảng cách không âm ) va x = 12 (nhận) suy ra chiều rộng bằng 12 - 7 = 5m
Vậy chiều dài bằng 12 và chiều rộng bằng 5
Mình chưa rõ bạn học lớp mấy nên sợ bài làm không phù hơp , nếu vậy bạn liên hệ để có cách giải phù hợp hơn
Chúc Thành Công

Gọi chiều dài mảnh vườn là a (m) (a>7)
chiểù rộng mảnh vườn là b (m) (b>0)
Theo bài ra : a^2+b^2=13^2=169 (định lí Py-ta-go)
Ta có (a-b)^2=7^2
=>a^2+b^2-2ab=49
=>-2ab=49-169=-120
=>ab=-120:-2=60 => diện tích mảnh vườn là 60 m2

- Gọi chiều dài hình chữ nhật đó là x ( m, x > 7 )
=> Chiều rộng hình chữ nhật đó là : x -7 ( m )
- Áp dụng định lý Pi ta go ta được :\(x^2+\left(x-7\right)^2=13^2\)
\(\Leftrightarrow x^2+x^2-14x+49-169=0\)
\(\Leftrightarrow2x^2-14x-120=0\)
\(\Leftrightarrow\left(x-12\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-5\end{matrix}\right.\)
=> x = 12 ( TM )
Vậy diện tích HCN đó là : x ( x - 7 ) = 60 ( m^2 )

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (0 < x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
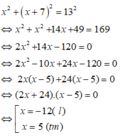
Vậy chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
Chọn đáp án C

A B C D
Ta có :
\(AD^2+CD^2=AC^2\)( ĐỊnh lý Pytago)
\(\Rightarrow2CD^2+49-14CD=169\)
\(2CD\left(CD-7\right)=120\)
\(CD\left(CD-7\right)=60\)
\(\Rightarrow S_{ABCD}=60\)