Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)
\(\Leftrightarrow2x-4-x-1=3x-11\)
\(\Leftrightarrow2x-x-3x=-11+1+4\)
\(\Leftrightarrow-2x=-6\)
\(\Leftrightarrow x=3\)
Gọi quãng đường người đi xe máy từ A đến B là x(km)(x>0)
thời gian người đi xe máy từ A đến B là \(\dfrac{x}{40}h\)
thời gian người đi xe máy trở về là\(\dfrac{x}{30}h\)
Theo đầu bài ta có phương trình
Đổi 45p=\(\dfrac{3}{4}h\)
\(\dfrac{x}{30}-\dfrac{x}{40}=\dfrac{3}{4}\)
\(\Leftrightarrow40x-30x=90\)
\(\Leftrightarrow10x=90\)
\(\Leftrightarrow x=9\left(tm\right)\)
Vậy quãng đường AB dài 9(km)

a: \(\Leftrightarrow20x^2-12x+15x+5< 10x\left(2x+1\right)-30\)
\(\Leftrightarrow20x^2+3x+5< 20x^2+10x-30\)
=>3x+5<10x-30
=>-7x<-35
hay x>5
b: \(\Leftrightarrow4\left(5x-20\right)-6\left(2x^2+x\right)>4x\left(1-3x\right)-15x\)
\(\Leftrightarrow20x-80-12x^2-6x>4x-12x^2-15x\)
=>14x-80>-11x
=>25x>80
hay x>16/5

Câu 3:
Gọi quãng đường AB là x ( km, x>0)
Thời gian lúc đi là: \(\dfrac{x}{30}h\)
Thời gian lúc về là: \(\dfrac{x}{40}h\)
45' = \(\dfrac{3}{4}h\)
Theo đề ra ta có pt:
\(\dfrac{x}{30}-\dfrac{3}{4}=\dfrac{x}{40}\)
\(\Leftrightarrow4x-90=3x\)
\(\Leftrightarrow x=90\) ( nhận)
Vậy quẵng đường AB dài 90 km

a: \(\Leftrightarrow1-x+3x+3=2x+3\)
=>2x+4=2x+3(vô lý)
b: \(\Leftrightarrow\left(x+2\right)^2-2x+3=x^2+10\)
\(\Leftrightarrow x^2+4x+4-2x+3=x^2+10\)
=>4x+7=10
hay x=3/4
d: \(\Leftrightarrow\left(-2x+5\right)\left(3x-1\right)+3\left(x-1\right)\left(x+1\right)=\left(x+2\right)\left(1-3x\right)\)
\(\Leftrightarrow-6x^2+2x+15x-5+3\left(x^2-1\right)=\left(x+2\right)\left(1-3x\right)\)
\(\Leftrightarrow-6x^2+17x-5+3x^2-3=x-3x^2+2-6x\)
\(\Leftrightarrow-3x^2+17x-8=-3x^2-5x+2\)
=>22x=10
hay x=5/11

a, \(6x^2-5x+3=2x-3x\left(3-2x\right)\)
⇔ \(6x^2-5x+3=2x-9x+6x^2\)
⇔ \(6x^2-5x+3-6x^2+9x-2x=0\)
⇔ \(2x+3=0\)
⇔ \(2x=-3\)
⇔ \(x=-\dfrac{3}{2}\)
b, \(\dfrac{2\left(x-4\right)}{4}-\dfrac{3+2x}{10}=x+\dfrac{1-x}{5}\)
⇔ \(\dfrac{20\left(x-4\right)}{4.10}-\dfrac{4\left(3+2x\right)}{4.10}=\dfrac{5x}{5}+\dfrac{1-x}{5}\)
⇔ \(\dfrac{20x-80}{40}-\dfrac{12+8x}{40}=\dfrac{5x+1-x}{5}\)
⇔ \(\dfrac{20x-80-12-8x}{40}=\dfrac{4x+1}{5}\)
⇔ \(\dfrac{12x-92}{40}-\dfrac{4x+1}{5}=0\)
⇔ \(\dfrac{12x-92}{40}-\dfrac{8\left(4x+1\right)}{40}=0\)
⇔ \(12x-92-8\left(4x+1\right)=0\)
⇔ 12x - 92 - 32x - 8 = 0
⇔ -100 - 20x = 0
⇔ 20x = -100
⇔ x = -100 : 20
⇔ x = -5

b: \(\Leftrightarrow\dfrac{7x+10}{x+1}\left(x^2-x-2-2x^2+3x+5\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(-x^2+2x+3\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(x^2-2x-3\right)=0\)
=>(7x+10)(x-3)=0
hay \(x\in\left\{-\dfrac{10}{7};3\right\}\)
d: \(\Leftrightarrow\dfrac{13}{2x^2+7x-6x-21}+\dfrac{1}{2x+7}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\dfrac{13}{\left(2x+7\right)\left(x-3\right)}+\dfrac{1}{\left(2x+7\right)}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow26x+91+x^2-9-12x-14=0\)
\(\Leftrightarrow x^2+14x+68=0\)
hay \(x\in\varnothing\)
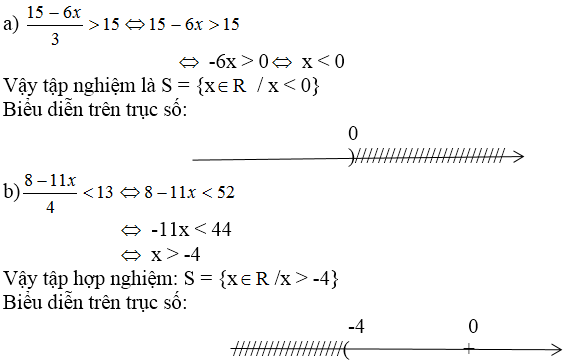
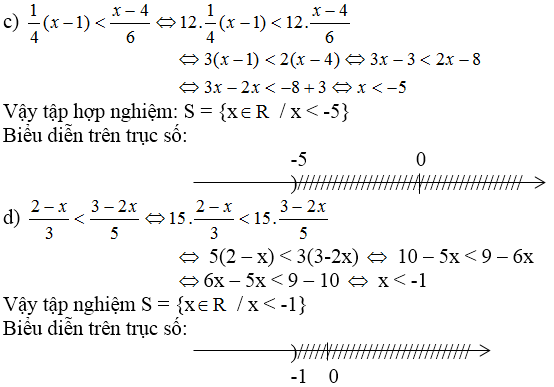



3) 9h30phút-30phút=9h
Gọi x(km) là quãng đường từ A đến B (ĐK X>0)
Thời gian xe đi từ A đến B là \(\dfrac{X}{15}\)(h)
Thời gian xe đi từ B đến A là \(\dfrac{X}{12}\)(h)
Theo đề bài ta có phương trình :
\(\dfrac{x}{15}+\dfrac{x}{12}=9\)
Giải pt:\(\dfrac{X}{15}+\dfrac{x}{12}=9\Leftrightarrow\dfrac{4x}{60}+\dfrac{5x}{60}=\dfrac{540}{60}\Rightarrow4x+5x=540\Leftrightarrow9x=540\Leftrightarrow x=60\)
Vậy quãng đường từ A đến B là 60 km
\(15x-3\left(3x-2\right)=45-5\left(2x-5\right)\Leftrightarrow15x-9x+6=45-10x+25\Leftrightarrow16x=64\Leftrightarrow x=4\)