Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

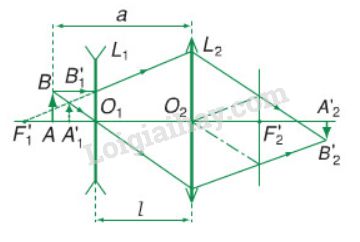
a) Sơ đồ tạo ảnh : ABL1⟶A1B1L2⟶A2B2AB⟶L1A1B1⟶L2A2B2
Hệ gồm hai thấu kính L1 và L2 đồng trục có tiêu điểm ảnh chính của (L1) trùng với tiêu điểm vật chính của L2=>a=O1O2=f1+f2L2=>a=O1O2=f1+f2
Chùm tia sáng tới song song: =>d1=∞=>d′1=f1=>d2=a−d′1=f2=>d1=∞=>d1′=f1=>d2=a−d1′=f2
=>d′2=∞=>d2′=∞
=> chùm tia ló ra khỏi (L2) cũng là chùm tia song song.
b) Vẽ đường đi của chùm tia sáng ứng với các trường hợp:
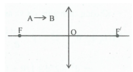
(L1 ) và (L2 ) đều là thấu kính hội tụ: hình 30.1
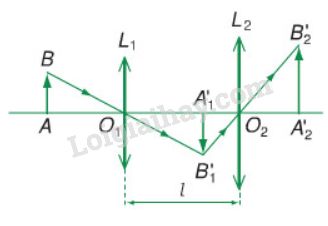
L1 là thấu kính hội tụ; L2 là thấu kính phân kì: Hình 30.2
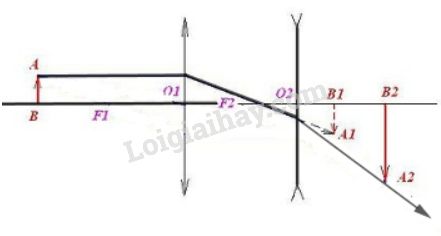
L1 là thấu kính phân kì; L2 là thấu kính hội tụ: Hình 30.3


+ Thấu kính dịch ra xa vật thì ảnh
dịch lại gần thấu kính. Vì thấu kính rời lại gần màn thêm 15 cm đồng thời màn cũng dời lại gần thấu kính thêm 15 cm nên:



a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
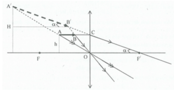
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!