Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này nhớ hôm trước làm rồi mà không nhớ ở câu nào nữa == , ngại tìm lại nên làm luôn :>
M I x C A O B D y
a) Ta có : OC , OD là các tia phân giác của 2 góc kề bù nên \(\widehat{COD}=90^o\) . Gọi I là trung điểm của CD tì :
IC = ID = IO
nên I là tâm và IO là bán kính của đường tròn có đường kính CD
b)
Chu vi hình thang ABDC bằng :
AB + AC + BD + CD
Ta dễ dàng chứng inh được :
AC + BD = CM + MD = CD
nên chu vi ABDC bằng AB + 2CD
Ta có AB không đổi nên chu vi ABDC nhỏ nhất và bằng 3AB .
c)
Đặt AC = x ; BD = y . Chu vi ABCD bằng :
AB + 2CD = 4 + 2( x + y )
Do chu vi ABDC bằng 14 nên :
4 + 2( x + y ) = 14
hay
x + y = 5 (1)
Ta lại có :
xy = MC . MD
= OM2 ( hệ thức lượng tam giác vuông COD )
nên xy = 22 = 4 (2)
Từ (1) , (2) suy ra :
\(x+\frac{4}{x}=5\Leftrightarrow x^2+4=5x\Leftrightarrow x^2-5x+4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\Leftrightarrow x=1;4\)
Vậy , nếu điểm C ( thuộc tia Ax ) cách điểm A là 1 cm hoặc 4 cm thì chu vi hình thang ABDC vẫn bằng 14cm

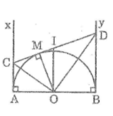
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.


c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm