Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

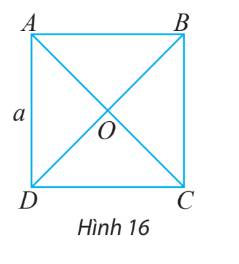
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).


\(\overrightarrow{u}=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{CM}+\overrightarrow{GB}+\overrightarrow{BN}\)
\(=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GB}+\overrightarrow{CM}+\overrightarrow{BN}=\overrightarrow{GB}+2\overrightarrow{BN}\)
G là trọng tâm \(\Rightarrow BG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{GB}+2\overrightarrow{BN}\right|\Rightarrow\left|\overrightarrow{u}\right|^2=BG^2+4BN^2+4\overrightarrow{GB}.\overrightarrow{BN}\)
\(=\dfrac{a^2}{3}+4a^2+4.\dfrac{a\sqrt{3}}{3}.a.cos120^0=\dfrac{13-2\sqrt{3}}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\sqrt{\dfrac{13-2\sqrt{3}}{3}}.a\)

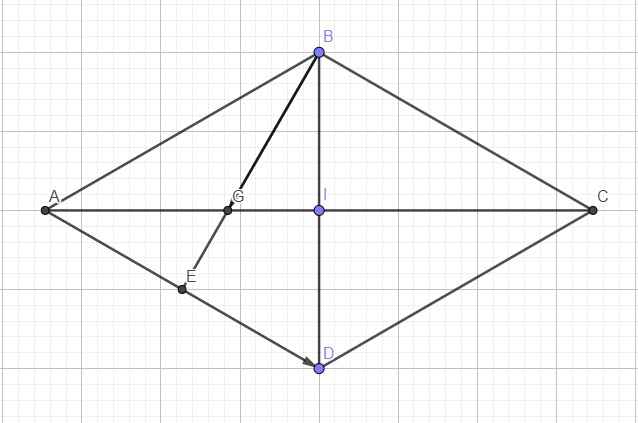
\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)

a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)

\(\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AC}.\overrightarrow{BC}=12\)
\(\Leftrightarrow\overrightarrow{BC}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=12\)
\(\Leftrightarrow\overrightarrow{BC}.\overrightarrow{BC}=12\)
\(\Rightarrow BC^2=12\Rightarrow BC=2\sqrt{3}\)

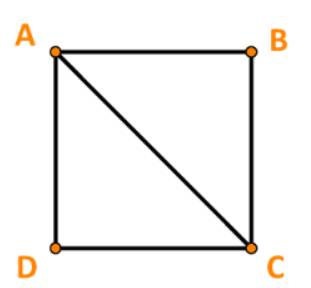
Ta có: \(|\overrightarrow {AB} | = AB\) và \(|\overrightarrow {AC} |\; = AC.\)
Mà \(AB = 3,\;AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)
\( \Rightarrow \;|\overrightarrow {AB} |\, = 3;\;\;|\overrightarrow {AC} |\, = 3\sqrt 2 \)