Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được

a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
c,Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
mình chỉ biết làm câu a và c thôi mong bạn thông cảm

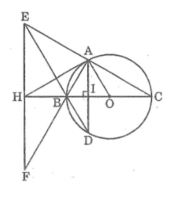
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.

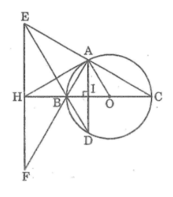

Bài 4:
a: Xét (O) cso
ΔABI nội tiếp
AI là đường kính
Do đo: ΔABI vuông tại B
Xét (O) có
ΔACI nội tiếp
AI là đường kính
Do đó: ΔACI vuông tại C
Xét tứ giác BHCI có
BH//CI
BI//CH
Do đó: BHCI là hình bình hành
b: Ta có: BHCI là hình bình hành
nên BC cắt HI tại trung điểm của mỗi đường
=>M là trung điểm chung của HI và BC
=>OM vuông góc với BC
c: Xét (O) có
ΔAKI nội tiếp
AI là đường kính
Do đó: ΔAKI vuông tại K
=>BC//KI
Xét ΔCHK có
CB vừa là đường cao, vừa là trung tuyến
nên ΔCHK cân tại C
=>CH=CK=BI
=>BKIC là hình thang cân