Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{8}+\dfrac{1}{d'}\)
\(\Leftrightarrow d'=-24\left(cm\right)\)
Chiều cao của ảnh:
\(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow h'=\dfrac{d'.h}{d}=\dfrac{-24.1}{8}=-3\left(cm\right)\)

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đén thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{20}=\dfrac{1}{d'}-\dfrac{1}{12}\)
\(\Rightarrow d'=7,5cm\)

Hướng dẫn:
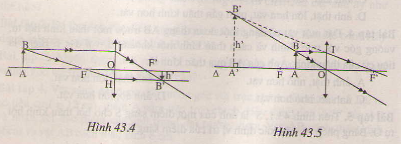
Nhận xét:
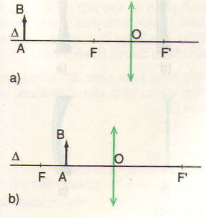
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
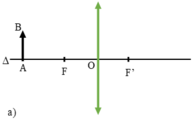
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:

Nhận xét:
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:

Nhận xét:
+ Vật AB cách thấu kính 36cm, ngoài khoảng tiêu cự, ảnh thật, ngược chiều vật
+ Khi vật AB cách thấu kính 8cm, trong khoảng tiêu cự, ảnh là ảo, cùng chiều vật và lớn hơn vật
Hướng dẫn:
Đặt một thấu kính hội tụ sát vào một trang sách, khi ấy các dòng chữ (coi là vật) sẽ nằm trong khoảng tiêu cự của thấu kính, cho hình ảnh các dòng chữ (là ảnh) sẽ cùng chiều và lớn hơn vật, do đó sẽ dễ đọc hơn. Từ từ dịch chuyển thấu kính ra xa, ảnh càng to và càng dễ đọc.
Tuy nhiên, khi dịch chuyển đến một vị trí nào đó, ta lại nhìn thấy ảnh của dòng chữ ngược chiều với vật. Đó là ảnh thật của dòng chữ tạo bởi thấu kính hội tụ. Vị trí đó trùng với tiêu điểm của thấu kính hội tụ, nên khi tiếp tục dịch chuyển ra xa thì dòng chữ (vật) nằm ngoài khoảng tiêu cự, cho ta ảnh ngược chiều, khó đọc

\(\left(1\right)\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OI}{A'B'}\) ( do \(OI=AB\) )
mik nhầm á bạn
a. Bạn tự vẽ ( ảnh ảo )
b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OI}{OA'}\) ( do OI = OA ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{5}{OA'}=\dfrac{8}{OA'+8}\)
\(\Leftrightarrow OA'=\dfrac{40}{3}\left(cm\right)\)
Thế \(OA'=\dfrac{40}{3}\) vào \(\left(1\right)\Leftrightarrow\dfrac{2}{A'B'}=5:\dfrac{40}{3}\)
\(\Leftrightarrow A'B'=\dfrac{16}{3}\left(cm\right)\)

Dựng ảnh của vật sáng AB qua thấu kính hội tụ. Dùng hai trong ba tia sáng đã học để dựng ảnh B’ của điểm B.
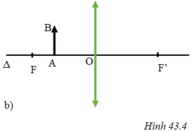
+ Vật AB cách thấu kính d = 36 cm, vật ngoài khoảng OF.
Tia BI đi song song với trục chính nên cho tia ló đi qua F’
Tia tới BO là tia đi quang tâm O nên cho tia ló đi thẳng
Hai tia ló trên giao nhau tại B’, ta thu được ảnh thật B’ của B qua thấu kính.
Từ B’ hạ vuông góc với trục của thấu kính, cắt trục chính tại điểm A’. A’ là ảnh của điểm A. A’B’ là ảnh của AB tạo bởi thấu kính hội tụ.
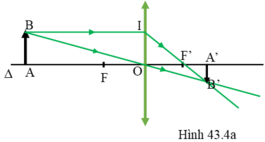
Nhận xét: Ảnh A’B” là ảnh thật ngược chiều với vật khi vật được đặt ngoài khoảng tiêu cự ( Hình 43.4a)
+ Vật AB cách thấu kính d = 8 cm, vật nằm trong khoảng OF.
Tia BI đi song song với trục chính nên cho tia ló đi qua F’
Tia tới BO là tia đi quang tâm O nên cho tia ló đi thẳng
Hai tia ló trên có đường kéo dài giao nhau tại B’, ta thu được ảnh ảo B’ của B qua thấu kính.
Từ B’ hạ vuông góc với trục của thấu kính, cắt trục chính tại điểm A’. A’ là ảnh của điểm A. A’B’ là ảnh của AB tạo bởi thấu kính hội tụ.
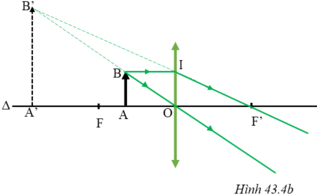
Nhận xét: Ảnh ảo A’B’ cùng chiều với vật và lớn hơn vật khi vật được đặt trong khoảng tiêu cự (Hình 43.4b)

Ảnh A'B' của vật AB tạo bởi thấu kính đã cho:
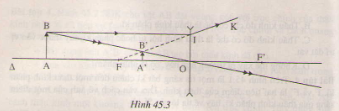
+ Ta dựa vào tia đi song song trục chính và tia đi qua quang tâm để dựng ảnh A'B' của AB. Khi tịnh tiến AB luôn vuông góc với trục chính thì tại mọi vị trí, tia BI luôn không đổi, cho tia ló IK cũng không đổi. Do đó tia BO luôn cắt tia IK kéo dài tại B' nằm trong đoạn FI. Chính vì vậy, ảnh A'B' luôn nằm trong khoảng tiêu cự của thấu kính.

Nó bị lỗi đó. Trc mk có để ý r sửa lại nhưng nó vẫn bị đấy thôi


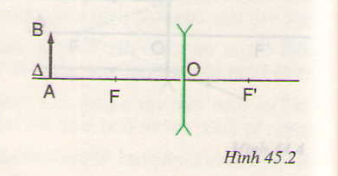
Từ hình vẽ ta thấy ảnh là ảnh ảo, cùng chiều, lớn hơn vật.
Xét hai tam giác AOB và A’OB’ ta có
Góc O chung; góc A = góc A’ = 900.
Nên tam giác AOB đồng dạng với tam giác A’OB’.
Ta có:\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{d}{d'}=\dfrac{AB}{A'B'}\)
Xét hai tam giác F’IO và tam giác F’A’B’. Ta có:
Góc F’ chung; góc O = góc A’ = 900
Nên tam giác F’IO đồng dạng với tam giác F’A’B’. Ta có:
\(\dfrac{F'O}{F'A'}=\dfrac{IO}{A'B'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{F'O}{F'O+OA'}=\dfrac{AB}{A'B'}=\dfrac{d}{d'}\)
\(\dfrac{f}{f+d'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{20}{20+d'}=\dfrac{12}{d'}\Leftrightarrow20d'=240+12d'\Leftrightarrow8d'=240\)
\(\Rightarrow d'=30cm\)
hình tham khảo