
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x+\dfrac{3}{2}=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}-\dfrac{3}{2}\)
\(x=3\)
Vậy x = 3 là giá trị cần tìm
b) \(\dfrac{1}{3}x+\dfrac{3}{4}x-75\%=-5\dfrac{1}{4}\)
\(x\left(\dfrac{1}{3}+\dfrac{3}{4}\right)-\dfrac{75}{100}=\dfrac{-19}{4}\)
\(x\left(\dfrac{4}{12}+\dfrac{9}{12}\right)-\dfrac{3}{4}=\dfrac{-19}{4}\)
\(x.\dfrac{13}{12}-\dfrac{3}{4}=\dfrac{-19}{4}\)
\(x.\dfrac{13}{12}=\dfrac{-19}{4}+\dfrac{3}{4}\)
\(x.\dfrac{13}{12}=-4\)
\(x=-4:\dfrac{13}{12}\)
\(x=-\dfrac{48}{13}\)
Vậy..................................
a) x + \(\dfrac{3}{2}\)= \(\dfrac{9}{2}\)
=> x= \(\dfrac{9}{2}\)- \(\dfrac{3}{2}\)
=> x=3
Vậy x=3
b) \(\dfrac{1}{3}\)x + \(\dfrac{3}{4}\)x - 75%= \(-5\dfrac{1}{4}\)
=> x.(\(\dfrac{1}{3}\)+ \(\dfrac{3}{4}\)) - \(\dfrac{3}{4}\)= \(\dfrac{-21}{4}\)
=> x. \(\dfrac{13}{12}\)- \(\dfrac{3}{4}\)=\(\dfrac{-21}{4}\)
=> x. \(\dfrac{13}{12}\)= \(\dfrac{-21}{4}\)+ \(\dfrac{3}{4}\)
=> x. \(\dfrac{13}{12}\)= \(\dfrac{-9}{2}\)
=> x= \(\dfrac{-9}{2}\): \(\dfrac{13}{12}\)= \(\dfrac{-9}{2}\). \(\dfrac{12}{13}\)
=> x= \(\dfrac{-54}{13}\)
Vậy x= \(\dfrac{-54}{13}\)

Ta có :
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1+3}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\)
\(B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3+3}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\)
Vì \(1+\dfrac{3}{10^{50}-1}< 1+\dfrac{3}{10^{50}-3}\Rightarrow A< B\)

\(a.x+9=2\frac{1}{3}\)
\(x=2\frac{1}{3}-9\)
\(x=-\frac{20}{3}\)
\(b.\frac{-5}{2}.x=\frac{1}{10}\)
\(x=\frac{1}{10}:\frac{-5}{2}\)
\(x=-\frac{1}{25}\)
a)
<=> x=\(\frac{7}{3}-9=-\frac{20}{3}\)
b)
<=> x=\(\frac{1}{10}:\frac{-5}{2}=-\frac{2}{25}\)

3S= 3/2.5+3/5.8+....+3/17.20
= (5-2)/2.5+(8-5)/5.8+....+(20-17)/17.20
= 1/2 - 1/5 + 1/5 - 1/8 + ...... + 1/17 - 1/20 = 1/2 - 1/20 = 9/20
=> S = 3/20
\(S=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{17.20}\)
\(S=\frac{1}{3}\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{17}-\frac{1}{20}\right)\)
\(S=\frac{1}{3}\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(S=\frac{1}{3}.\frac{9}{20}\)
\(S=\frac{3}{20}\)

\(S=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{17.20}\)
\(S=3.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{17}-\frac{1}{20}\right)\)
\(S=3.\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(S=3.\frac{9}{20}=\frac{27}{20}\)

\(a.\frac{2}{3}+\frac{5}{7}=\frac{14}{21}+\frac{15}{21}=\frac{19}{21}\)
\(b.\frac{3}{2}.\frac{4}{5}-\frac{1}{35}=\frac{6}{5}-\frac{1}{35}=\frac{42}{35}-\frac{1}{35}=\frac{41}{35}\)
\(c.\left(\frac{20}{3}-\frac{22}{5}\right):\frac{1}{15}=\left(\frac{100}{15}-\frac{66}{15}\right):\frac{1}{15}=\frac{34}{15}:\frac{1}{15}=\frac{34}{15}x15=34\)
a) \(\frac{2}{3}+\frac{5}{7}=\frac{14}{21}+\frac{15}{21}=\frac{14+15}{21}=\frac{29}{21}\)
b)\(\frac{3}{2}.\frac{4}{5}-\frac{13}{5}=\frac{3.4}{2.5}-\frac{13}{5}=\frac{12}{10}-\frac{13}{5}=\frac{6}{5}-\frac{13}{5}=-\frac{7}{5}\)
c)\(\left(\frac{20}{3}-\frac{22}{5}\right):\frac{1}{15}=\left(\frac{100}{15}-\frac{66}{15}\right):\frac{1}{15}=\frac{44}{15}.15=44\)

\(A=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+.....+\frac{1}{50^2}\)
\(A=\frac{1}{1^2}+\frac{1}{2\times2}+\frac{1}{3\times3}+\frac{1}{4\times4}+.....+\frac{1}{50\times50}\)
\(A< \frac{1}{1}+\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+.....+\frac{1}{49\times50}\)
\(A< 1+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+.....+\frac{1}{49}-\frac{1}{50}\)
\(A< 2-\frac{1}{50}\)
\(2-\frac{1}{50}< 2\)
\(\Rightarrow A< 2\)
Chúc bạn học tốt![]()
ta có: \(\frac{1}{2^2}=\frac{1}{2.2}< \frac{1}{1.2};\frac{1}{3^2}=\frac{1}{3.3}< \frac{1}{2.3};\frac{1}{4^2}=\frac{1}{4.4}< \frac{1}{3.4};...;\frac{1}{100^2}=\frac{1}{100.100}< \frac{1}{99.100}\)
=>

Dễ thấy:
\(\dfrac{1}{1^2}=\dfrac{1}{1.1}=\dfrac{1}{1}=1\)
\(\dfrac{1}{2^2}=\dfrac{1}{2.2}< \dfrac{1}{1.2}\)
\(.....................\)
\(\dfrac{1}{50^2}=\dfrac{1}{50.50}< \dfrac{1}{49.50}\)
Cộng các vế trên với nhau ta được:
\(A< 1+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\right)\)
\(\Rightarrow A< 1+\) \(\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
\(\Rightarrow A< 1+\left(1-\dfrac{1}{50}\right)\)
\(\Rightarrow A< 1+1-\dfrac{1}{50}=2-\dfrac{1}{50}\)
Mà \(2-\dfrac{1}{50}< 2\Leftrightarrow A< 2\)
Vậy \(A=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{50^2}< 2\) (Đpcm)

Ta có :
\(A=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+.........+\dfrac{1}{50^2}\)
Ta thấy :
\(\dfrac{1}{1^2}=1\)
\(\dfrac{1}{2^2}=\dfrac{1}{2.2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}=\dfrac{1}{3.3}< \dfrac{1}{2.3}\)
\(..............\)
\(\dfrac{1}{50^2}=\dfrac{1}{50.50}< \dfrac{1}{49.50}\)
\(\Rightarrow A< 1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+..........+\dfrac{1}{49.50}\)
\(A< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...........+\dfrac{1}{49}-\dfrac{1}{50}\)
\(A< 1+1-\dfrac{1}{50}\)
\(A< 2-\dfrac{1}{50}\)
\(\Rightarrow A< 2\rightarrowđpcm\)



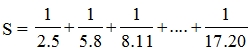


 chung minh A<2
chung minh A<2
a) \(x+\frac{3}{2}=\frac{9}{2}\)
\(\Rightarrow x=\frac{9}{2}-\frac{3}{2}=\frac{6}{2}=3\)
b) \(\frac{1}{3}x+\frac{3}{4}x-75\%=-5\frac{1}{4}\)
\(\Leftrightarrow\frac{4x}{12}+\frac{9x}{12}-\frac{9}{12}=-\frac{63}{12}\)
\(\Leftrightarrow\frac{13x-9}{12}=\frac{-63}{12}\)
\(\Rightarrow13x-9=-63\)
\(13x=-54\Rightarrow x=\frac{-54}{13}\)
a) \(x+\frac{3}{2}=\frac{9}{2}\)
\(\Rightarrow x=\frac{9}{2}-\frac{3}{2}\)
\(\Rightarrow x=\frac{6}{2}=3\)