Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
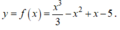
Ta có f ' x = x 2 - 2 x + 1 .
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.

1.
Xét \(x^2-mx+m=0\) (1)
\(\Delta=m^2-4m\)
Hàm có đúng 1 tiệm cận đứng khi:
TH1: \(\Delta=0\Leftrightarrow\left[{}\begin{matrix}m=0\\m=4\end{matrix}\right.\)
Th2: (1) có 1 nghiệm \(x=1\)
\(\Leftrightarrow1-m+m=0\left(ktm\right)\)
Vậy \(m\in\left\{0;4\right\}\)
2.
\(\Leftrightarrow m=\frac{x^3+x^2+x}{\left(x^2+1\right)^2}\)
Xét hàm \(f\left(x\right)=\frac{x^3+x^2+x}{\left(x^2+1\right)^2}\Rightarrow f'\left(x\right)=\frac{\left(1-x\right)\left(x+1\right)^2}{\left(x^2+1\right)^3}\ge0;\forall x\in\left[0;1\right]\)
Hàm đồng biến trên [0;1] \(\Rightarrow f\left(0\right)\le m\le f\left(1\right)\Leftrightarrow0\le m\le\frac{3}{4}\)
3.
\(y'=-2sin2x-4sinx=0\Leftrightarrow sinx=0\)
\(\Rightarrow x=k\pi\)
\(y\left(0\right)=6\) ; \(y\left(\pi\right)=-2\)
\(\Rightarrow M=6\)
4.
\(y'=\frac{-1}{\left(x-1\right)^2}< 0\Rightarrow\) hàm số nghịch biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(1;+\infty\right)\)
5.
\(y'=\frac{-m\left(m-1\right)+2}{\left(sinx-m\right)^2}.cosx< 0\Leftrightarrow-m^2+m+2< 0\)
\(\Leftrightarrow m\in\left(-\infty;-1\right)\cup\left(2;+\infty\right)\)

Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.

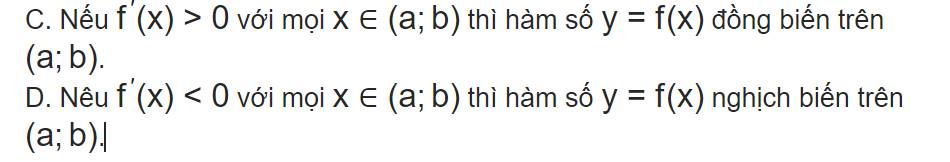
Đúng rồi bạn, nếu làm tự luận thì làm như vầy
Đằng thức xảy ra khi và chỉ khi cả 3 bình phương bằng 0
Làm trắc nghiệm thì nghĩ tới dáng đồ thị của hàm bậc 3 chọn luôn kết quả D
Mình cũng ko biết, chắc nó nảy sinh từ việc nắm vững lý thuyết về đồ thị hàm bậc 3, hàm này có 2-3 kiểu đồ thị thôi mà, nhìn vào thấy liền