A. 2cm. B. 4cm. C.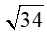 cm. D. 8cm.
cm. D. 8cm.
Câu 4: Tích của hai đơn thức 7x2y và (–xy) bằng
A. –7x3y2. B. 7x3y2. C. –7x2y. D. 6x3y2.
Câu 5: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây là ba cạnh của một tam giác?
A. 2cm; 3cm; 6cm. B. 3cm; 4cm; 6cm. C. 2cm; 4cm; 6cm. D. 2cm; 3cm; 5cm.
Câu 6: Đơn thức nào sau đây đồng dạng với đơn thức –3x2y3?
A. –3x3y2. B. 3(xy)2. C. –xy3. D. x2y3.
Câu 7: Tam giác ABC cân tại A có 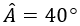 khi đó số đo của góc B bằng
khi đó số đo của góc B bằng
A. 1000 B. 500 C. 700 D. 400
Câu 8: Bậc của đa thức 12x5y – 2x7 + x2y6 là
A. 5. B. 12. C. 7. D. 8.
Câu 9: Tam giác ABC có AB < AC < BC. Khẳng định nào sau đây là đúng?
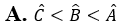
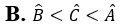
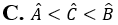
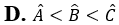
Câu 10: Giá trị của biểu thức 2x2 – 5x + 1 tại x = –1 là
A. –2. B. 8. C. 0. D. –6.
Câu 11: Tam giác ABC có BM là đường trung tuyến và G là trọng tâm. Khẳng định nào sau đây là đúng?
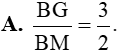
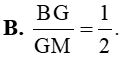
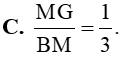
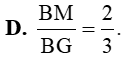
Câu 12: Thu gọn đa thức P = – 2x2y – 4xy2 + 3x2y + 4xy2 được kết quả là
A. P = x2y. B. P = – 5x2y. C. P = – x2y. D. P = x2y – 8xy2.
Câu 13: Tam giác ABC vuông tại A có AB < AC. Vẽ AH vuông góc với BC 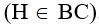 . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?
A. HB < HC. B. HC < HB. C. AB < AH. D. AC < AH.
Câu 14: Nghiệm của đa thức f(x) = 2x – 8 là
A. –6. B. –4. C. 0. D. 4.
Câu 15: Cho 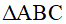 và
và 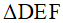 có
có 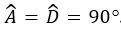 . Để kết luận
. Để kết luận 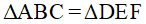 theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?
theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?
A. BC = EF; 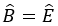
C. AB = DE; AC = DF.
B. BC = EF; AC = DF.
D. BC = DE; 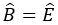
II. TỰ LUẬN: (5,0 điểm).
Bài 1: (1,25 điểm).
Học sinh lớp 7A góp tiền ủng hộ cho trẻ em khuyết tật. Số tiền đóng góp của mỗi học sinh được ghi ở bảng thống kê sau (đơn vị là nghìn đồng).
| 5 | 7 | 9 | 5 | 8 | 10 | 5 | 9 | 6 | 10 | 7 | 10 | 6 | 10 | 7 | 6 | 8 | 5 |
| 6 | 8 | 10 | 5 | 7 | 7 | 10 | 7 | 8 | 5 | 8 | 7 | 8 | 5 | 9 | 7 | 10 | 9 |
a) Dấu hiệu ở đây là gì?
b) Lập bảng “tần số”.
c) Tính số trung bình cộng (làm tròn đến chữ số thập phân thứ nhất).
Bài 2: (1,25 điểm).
a) Cho hai đa thức A(x) = 2x2 – x3 + x – 3 và B(x) = x3 – x2 + 4 – 3x.
Tính P(x) = A(x) + B(x).
b) Cho đa thức Q(x) = 5x2 – 5 + a2 + ax. Tìm các giá trị của a để Q(x) có nghiệm x = – 1.
Bài 3: (2,5 điểm).
Cho 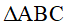 vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.
vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.
a) Chứng minh 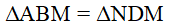 .
.
b) Chứng minh BE = DE.
c) Chứng minh rằng MN < MC.






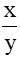
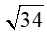 cm. D. 8cm.
cm. D. 8cm.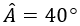 khi đó số đo của góc B bằng
khi đó số đo của góc B bằng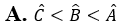
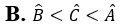
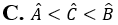
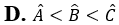
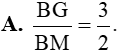
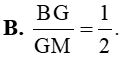
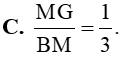
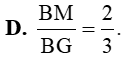
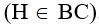 . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?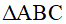 và
và 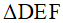 có
có 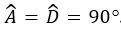 . Để kết luận
. Để kết luận 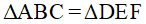 theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?
theo trường hợp cạnh huyền – cạnh góc vuông, cần có thêm điều kiện nào sau đây?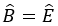
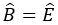
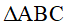 vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.
vuông tại A (AB < AC), tia phân giác của góc B cắt AC tại M. Trên tia đối của tia MB lấy điểm D sao cho MB = MD, từ điểm D vẽ đường thẳng vuông góc với AC tại N và cắt BC tại điểm E.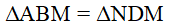 .
.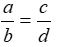 (a, b, c, d # 0) ta có thể suy ra:
(a, b, c, d # 0) ta có thể suy ra: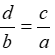 B.
B. 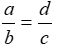
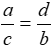 D.
D.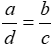
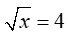 thì x bằng:
thì x bằng: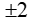 B.
B. 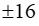 C. 2 D.16
C. 2 D.16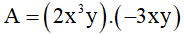
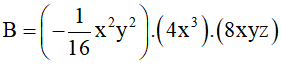
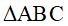 vuông tại A, có AB = 6cm, AC = 8cm.
vuông tại A, có AB = 6cm, AC = 8cm.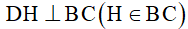 .
.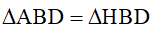
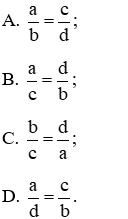
trắc nghiệm:
1D
2C
3B
4A
5B
6D
7C
8D
9A
10B
11C
12A
13A
14D
15A