Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
b; góc xAC=góc ABC
=>góc xAC=góc ADE
=>xy//DE

a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: Xét ΔHQB và ΔHPC có
góc HQB=góc HPC
góc QHB=góc PHC
=>ΔHQB đồng dạng với ΔHPC
=>HQ/HP=HB/HC
=>HQ*HC=HP*HB
c: kẻ tiếp tuyến Ax
=>góc xAC=góc ABC=góc ADE
=>Ax//ED
=>OA vuông góc DE

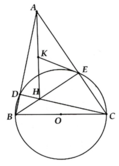
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm

1.
Chứng minh được \widehat{CEB} = \widehat{BDC} = 90^{\circ}CEB=BDC=90∘.
Suy ra 44 điểm B,E, D, CB,E,D,C cùng thuộc đường tròn đường kính CBCB nên tứ giác BCDEBCDE nội tiếp.
Có tứ giác BCDEBCDE nội tiếp nên \widehat{DCE} = \widehat{DBE}DCE=DBE (22 góc nội tiếp cùng chắn cung DEDE) hay \widehat{ACQ} = \widehat{ABP}ACQ=ABP.
Trong đường tròn tâm (O)(O), ta có \widehat{ACQ}ACQ là góc nội tiếp chắn cung AQAQ và \widehat{ABP}ABP nội tiếp chắn cung APAP
\Rightarrow \overset{\frown}{AQ}=\overset{\frown}{AP}⇒AQ⌢=AP⌢.
2.
(O)(O) có \overset{\frown}{AQ}=\overset{\frown}{AP}AQ⌢=AP⌢ nên \widehat{ABP} = \widehat{ABQ}ABP=ABQ hay \widehat{HBE} = \widehat{QBE}HBE=QBE.
Ta chứng minh được BEBE vừa là đường cao, vừa là phân giác của tam giác HBQHBQ nên EE là trung điểm của HQHQ.
Chứng minh tương tự DD là trung điểm của HPHP \Rightarrow DE⇒DE là đường trung bình của tam giác HPQHPQ \Rightarrow DE // PQ⇒DE//PQ (1).
Do \overset{\frown}{AQ}=\overset{\frown}{AP}AQ⌢=AP⌢ nên AA là điểm chính giữa cung PQPQ \Rightarrow OA \perp PQ⇒OA⊥PQ (2).
Từ (1) và (2) suy ra OA \perp DEOA⊥DE.
3.
Kẻ đường kính CFCF của đường tròn tâm (O)(O), chứng minh tứ giác ADHEADHE nội tiếp đường tròn đường kính AHAH.
Chứng minh tứ giác AFBHAFBH là hình bình hành, suy ra BF=AHBF=AH.
Trong đường tròn (O)(O) có \widehat{CAB} = \widehat{CFB} = 60^{\circ}CAB=CFB=60∘ (2 góc nội tiếp cùng chắn cung BCBC). Chỉ ra tam giác BCFBCF vuông tại BB và áp dụng hệ thức giữa cạnh và góc ta được BF=CF. \cos 60^{\circ} =R=6BF=CF.cos60∘=R=6 cm.
Đường tròn ngoại tiếp tứ giác ADHEADHE cũng là đường tròn ngoại tiếp tam giác ADEADE.
Gọi rr là bán kính đường tròn ngoại tiếp tam giác ADEADE.
Suy ra 2r=AH=BF=62r=AH=BF=6 cm.
Vậy r=3r=3 cm.

c) Kẻ tiếp tuyến Ax của (O) ta có ^xAB = ^ACB (=1/2 cung AB)
Lại có tứ giác BEDC nội tiếp (vì ^D = ^E = 90 độ)
Mà ^AED = ^ ACB (Cùng bù với ^BED)
=> ^xAB = ^AED, mà ^xAB và ^AED ở vị trí SLT nên Ax// DE nhưng Ax vuông góc với OA (T/c Tiếp tuyến)
=> DE vuông góc với AO



sao chụy là cô giáo mà chụy hỏi nhiều zậy
Bài 1:
b)
chứng minh EDCB là tgnt => góc AED = góc ACB
từ đó, chứng minh tam giác AED đồng dạng ACB (gg)
=> DE / BC = AD / AB
tam giác ADB vuông tại A => AD / AB = cotg A = cotg 45 = 1
c)
kẻ tiếp tuyến tại Ax của (O) (Ax thuộc nửa mp bờ AC chứa B)
góc xAB = ACB = AED
=> DE // Ax
Mà Ax vuông góc với OA nên OA vuông góc với DE. (đpcm)