Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b.xét tổng hàng phần trăm của mỗi số ta có: 9+5+c=21 suy ra c=7
xét tổng hàng phần mười ta có : 3+b+b=7-2(do hàng phần trăm mượn đi 2) suy ra 3+2b=5 suy ra b=1
xét tổng hàng đơn vị ta có: a+3+8=16 suy ra a=5
thử thay a=5,b=1,c=7 vào a,39+3,b5+8,bc ta có: 5,39+3,15+8,17=16,71( thỏa mãn)
vậy abc=517

a) Viết phân số \(\frac{3}{5}\) dưới dạng phân số thập phân có mẫu là 10 và có mẫu số là 100 :
\(\frac{3}{5}=\frac{3\times2}{5\times2}=\frac{6}{10};\frac{3}{5}=\frac{3\times20}{5\times20}=\frac{60}{100}\)
b) Viết hai phân số thập phân mới tìm được thành hai số thập phân :
\(\frac{6}{10}=0,6;\frac{60}{100}=0,6\)
c) Có thế viết \(\frac{3}{5}\)thành số thập phân : \(0,6\).
#Y/n

Ta có sơ đồ:
a/b: 6 phần
c/d: 5 phần
a/b=1/15:(6+5)x6=2/55
c/d=2/55-1/15=1/33
hk tốt
b) Ta có: \(\frac{a}{b}=\frac{6}{5}\times\frac{c}{d}\)
Thay \(\frac{a}{b}=\frac{6}{5}\times\frac{c}{d}\)vào biểu thức \(\frac{a}{b}-\frac{c}{d}=\frac{1}{15}\)
Ta lại có: \(\frac{6}{5}\times\frac{c}{d}-\frac{c}{d}=\frac{1}{15}\)
\(\left(\frac{6}{5}-1\right)\times\frac{c}{d}=\frac{1}{15}\)
\(\frac{1}{5}\times\frac{c}{d}=\frac{1}{15}\)
\(\frac{c}{d}=\frac{1}{15}:\frac{1}{5}=\frac{1}{3}\)
Suy ra: \(\frac{a}{b}=\frac{6}{5}\times\frac{c}{d}=\frac{6}{5}\times\frac{1}{3}=\frac{2}{5}\)
Vậy.....

Bạn ghi rõ diện tích tam giác là bao nhiêu m2 và cạnh đáy dài bao nhiêu m ra nhé:)

Gọi hai phân số cần tìm lần lượt là x, y
Theo bài ra, ta có: \(\frac{x}{y}=\frac{13}{12}\) => \(x=\frac{13}{12}\times y\)
Nếu thêm vào phân số bị chia 5/6 và giữ nguyên phân số chia thì được thương là 51/24
=> (x + 5/6) : y = 51/24 => \(x+\frac{5}{6}=\frac{51}{24}\times y\)
<=> \(\frac{13}{12}\times y+\frac{5}{6}=\frac{51}{24}\times y\)
<=> \(\left(\frac{51}{24}-\frac{13}{12}\right)\times y=\frac{5}{6}\)
<=> \(\frac{25}{24}\times y=\frac{5}{6}\)
<=> \(y=\frac{4}{5}\)
=> \(x=\frac{13}{12}\times\frac{4}{5}=\frac{13}{15}\)
Vậy hai phân số đó là: 4/5 và 13/15

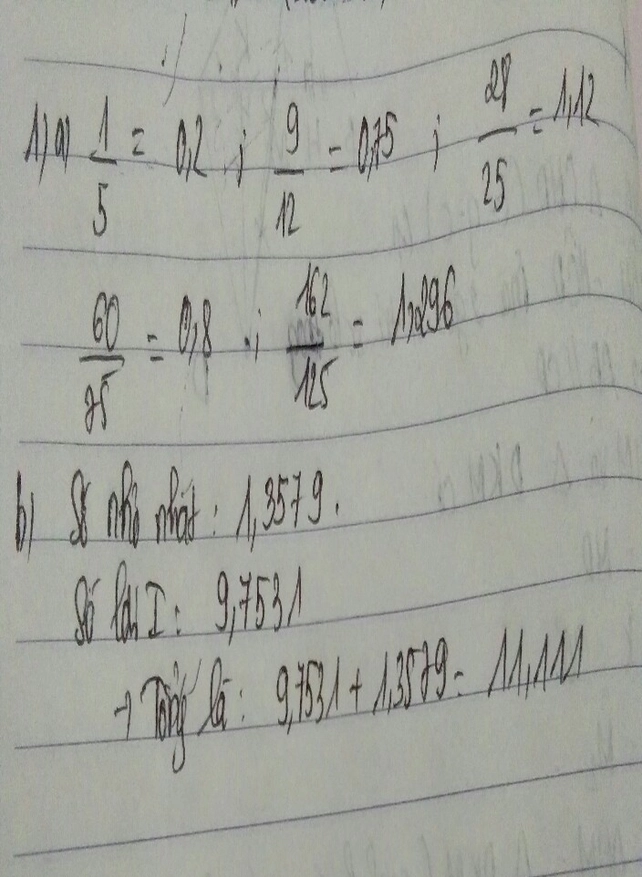
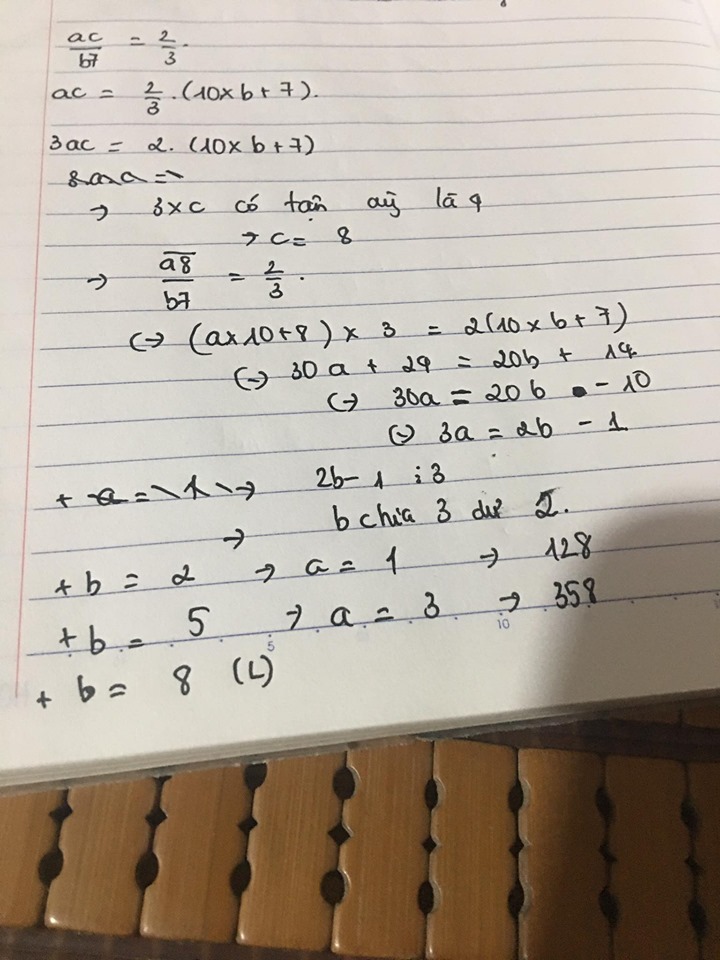

Chọn A nhé
vì số bóng đỏ là 30-6-15=9
ps bóng đỏ là 9:30=3/10
Đáp án: A.\(\frac{3}{10}\)