
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=12\left(83+17\right)=12.100=1200\)
b) \(B=-11\)
c) \(C=14+50=64\)
d) \(D=35-35+45=45\)

Bài 4:
a) \(x+xy-3y=4\)
\(\Leftrightarrow x-3+y\left(x-3\right)=1\)
\(\Leftrightarrow\left(x+y\right)\left(x-3\right)=1\)
mà \(x.y\)là số nguyên nên ta có bảng giá trị:
| x+y | 1 | -1 |
| x-3 | 1 | -1 |
| x | 4 | 2 |
| y | -3 | -3 |
b) \(BCNN\left(6,7\right)=42\)nên \(BC\left(6,7\right)=B\left(42\right)\).
\(200< 6k< 2000\Rightarrow33< k< 334\)
suy ra có \(334-33-1=300\)giá trị của \(x\)là bội của \(6\)mà \(200< x< 2000\).
\(200< 7l< 2000\Rightarrow28< l< 286\)
suy ra có \(286-28-1=257\)giá trị của \(x\)là bội của \(7\)mà \(200< x< 2000\).
\(200< 42m< 2000\Leftrightarrow4< m< 48\)
suy ra có \(48-4-1=43\)giá trị của \(x\)là bội của \(42\)mà \(200< x< 2000\)
Số giá trị của \(x\)thỏa mãn ycbt là: \(300+257-43=514\)(số)

Bài 5:
a) \(23⋮\left(x-2\right)\Leftrightarrow x-2\inƯ\left(23\right)=\left\{-23,-1,1,23\right\}\)
\(\Leftrightarrow x\in\left\{-21,1,3,25\right\}\).
b) \(2x+1\inƯ\left(-12\right)\)mà \(2x+1\)là số lẻ nên \(2x+1\in\left\{-3,-1,1,3\right\}\)
\(\Leftrightarrow x\in\left\{-2,-1,0,1\right\}\).
c) \(x-1=x+2-3⋮\left(x+2\right)\Leftrightarrow3⋮\left(x+2\right)\)
mà \(x\)là số nguyên nên \(x+2\inƯ\left(3\right)=\left\{-3,-1,1,3\right\}\Leftrightarrow x\in\left\{-5,-3,-1,1\right\}\).
Bài 4:
a) \(-18⋮3,15⋮3\Rightarrow-18a+15b⋮3\).
b) Theo a) ta có \(-18a+15b⋮3\)mà \(-2015⋮̸3\)nên không tồn tại hai số nguyên \(a,b\)thỏa mãn ycbt.

TL:
\(2x^3+16=32\)
\(2x^3=32-16\)
\(2x^3=16\)
\(x^3=16:2\)
\(x^3=8\)
\(x^3=2^3\)
\(\Rightarrow x=2\)
HT!~!


\(\left(x-2\right)\left(x-4\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2< 0\\x-4>0\end{matrix}\right.=>4< x< 2\left(1\right)\\\left\{{}\begin{matrix}x-2>0\\x-4< 0\end{matrix}\right.=>2< x< 4\left(2\right)}\end{matrix}\right.\)(1 ) vô lý=> loại
=> (x-2).(x-4)<0 <=> 2<x<4
b. ta có\(x^2+1>0\forall x\)
=>(x2 -1).(x2+1)<0 <=> (x2 -1)<0 <=> x2<1
<=> -1<x<1
câu c bạn làm tương tự

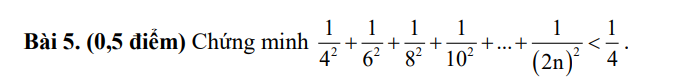






\(\Rightarrow A=\dfrac{1}{\left(2\cdot2\right)^2}+\dfrac{1}{\left(2\cdot3\right)^2}+\dfrac{1}{\left(2\cdot4\right)^2}+...+\dfrac{1}{\left(2n\right)^2}\\ A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\right)< \dfrac{1}{4}\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{\left(n-1\right)n}\right)\\ A< \dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{\left(n-1\right)}-\dfrac{1}{n}\right)\\ A< \dfrac{1}{4}\left(1-\dfrac{1}{n}\right)< \dfrac{1}{4}\left(\text{đ}pcm\right)\)