Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D 1 2 1
Trong \(\Delta\)ABC có: ^A = ^B +2.^C => ^A > ^B và ^A > ^C => BC là cạnh lớn nhất trong tam giác ABC.
+) Xét trường hợp: AB < AC < BC. Khi đó; ta đặt: AB = a; AC = a+1; BC = a+2 (Với a thuộc N*)
Trên cạnh BC lấy điểm D sao cho ^BAD = ^ACB, hay ^A1 = ^C (theo hình vẽ)
Xét \(\Delta\)ABC và \(\Delta\)DBA có: ^A1 = ^C; ^B chung => \(\Delta\)ABC ~ \(\Delta\)DBA (g.g)
=> \(\frac{AB}{DB}=\frac{BC}{BA}\)=> AB2 = BC.BD hay a2 = (a+2).BD (*)
Ta thấy: ^BAC = ^B + 2.^C; ^BAC = ^A1 + ^A2 = ^C + ^A2 => ^B + 2.^C = ^C + A2 <=> ^B + ^C = ^A2 (1)
Do ^D1 là góc ngoài \(\Delta\)BAD nên ^D1 = ^A1 + ^B = ^B + ^C (Vì ^C = ^A1) (2)
Từ (1) và (2) => ^D1 = ^A2 => \(\Delta\)ACD cân tại C => AC= CD = a+1 => BD = BC - CD = BC - AC = a+2 - a - 1 = 1
Thay BD = 1 vào (*) ta có:
\(a^2=\left(a+2\right).1\Leftrightarrow a^2-a-2=0\Leftrightarrow a^2+a-2a-2=0\)
\(\Leftrightarrow a\left(a+1\right)-2\left(a+1\right)=0\Leftrightarrow\left(a+1\right)\left(a-2\right)=0\Leftrightarrow\orbr{\begin{cases}a=-1\\a=2\end{cases}}\)
=> a = 2. (Loại TH a = -1 vì a thuộc N*) => a+1 = 3; a+2 = 4
Hay AB = 2; AC = 3; BC = 4
+) Xét trường hợp AC < AB < BC. Đặt AC = a; AB = a+1; BC = a+2
Chứng ming tương tự TH 1; ta có: AB2 = BC.BD; BD = BC - CD = BC - AC = a+2 - a = 2
Hay \(\left(a+1\right)^2=2\left(a+2\right)\)
\(\Leftrightarrow a^2+2a+1=2a+4\Leftrightarrow a^2=3\Leftrightarrow a=\pm\sqrt{3}\)(loại vì a thuộc N*)
Vậy độ dài 3 cạnh trong \(\Delta\)ABC t/m đề là AB = 2; AC = 3; BC = 4.


Giả sử \(\Delta ABC\)đều ngoại tiếp đường tròn (I), khi đó ta cần tính BC (hoặc AB, AC đều được)
Kẻ đường cao AH của \(\Delta ABC\). Nối B với I.
Ta ngay lập tức có BI là tia phân giác của \(\widehat{ABC}\)(vì I là tâm đường tròn nội tiếp \(\Delta ABC\))
Mà \(\widehat{ABC}=60^0\)(do \(\Delta ABC\)đều) \(\Rightarrow\widehat{IBH}=\frac{60^0}{2}=30^0\)
\(\Delta IBH\)vuông tại H \(\Rightarrow BH=IH.\cot\widehat{IBH}=r.\cot30^0=r\sqrt{3}\)
Mặt khác \(\Delta ABC\)đều có đường cao AH \(\Rightarrow\)AH cũng là trung tuyến \(\Rightarrow\)H là trung điểm BC
\(\Rightarrow BC=2BH=2r\sqrt{3}\)\(\Rightarrow\)Chọn ý thứ ba.

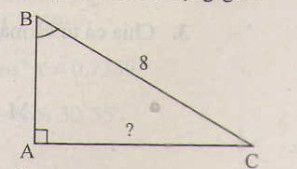
Xét \(\Delta\)ABC có :
AH2 = BH.CH
AH2 = c'.b' (1)
Mà c'/b' = 1/3
=》3c' = b
Thay vào (1) ta có :
12 = c'.3c'
12 = 3c'2
c'2 = 4
=》 c' = 2 (cm)
=》b' = 3.2 = 6(cm)
=》 BC = 2 + 6 = 8 (cm)
Ta có : AB2 = BH.BC = 2.8 = 16
=》 AB = 4(cm)
Lại có AC2 = CH.BC = 6.8 = 48(cm)
=》 AC = 4\(\sqrt{ }\)3 (cm)

Theo giả thiết có : \(abc\ne0\)chia hai vế của phương trình cho \(abc\)có : \(\frac{2ab+3bc+4ac}{abc}=\frac{5abc}{abc}\Leftrightarrow\frac{2}{a}+\frac{3}{b}+\frac{4}{c}=1\)
Xét : (ở tử của p tắc 7 = 4+3; 6= 4+2; 5=2+3 rồi nhóm nhân tử chung)
\(P=\frac{7}{a+b-c}+\frac{6}{b+c-a}+\frac{5}{c+a-b}\)
\(=\frac{4}{a+b-c}+\frac{3}{a+b-c}+\frac{4}{b+c-a}+\frac{2}{b+c-a}+\frac{3}{c+a-b}+\frac{2}{c+a-b}\)
\(=4\left(\frac{1}{a+b-c}+\frac{1}{b+c-a}\right)+3\left(\frac{1}{a+b-c}+\frac{1}{c+a-b}\right)+2\left(\frac{1}{b+c-a}+\frac{1}{c+a-b}\right)\)
Nếu có \(x,y\left(x>0,y>0\right)\)ta luôn có \(\left(x+y\right)^2\ge4xy\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
áp dụng vào P có
\(\frac{1}{a+b-c}+\frac{1}{b+c-a}\ge\frac{4}{a+b-c+b+c-a}=\frac{4}{2b}=\frac{2}{b}\)
\(\frac{1}{a+b-c}+\frac{1}{c+a-b}\ge\frac{4}{a+b-c+c+a-b}=\frac{4}{2a}=\frac{2}{a}\)
\(\frac{1}{b+c-a}+\frac{1}{c+a-b}\ge\frac{4}{b+c-a+c+a-b}=\frac{4}{2c}=\frac{2}{c}\)
Cộng từng vế của 3 bất đẳng thức :
\(P\ge4.\frac{2}{b}+3.\frac{2}{a}+2.\frac{2}{c}=2\left(\frac{4}{b}+\frac{3}{a}+\frac{2}{c}\right)=2.5=10\)
Vậy \(P_{min}=10\)dấu "=" sảy ra khi \(a=b=c=\frac{9}{5}\)
trên đầu mình viết nhầm nhe chỗ tổng phân số bằng 5 chứ ko phải 1

A B C M 2cm 2cm 2cm
a) Vì AM là trung tuyến của \(\Delta ABC\)tại A \(\Rightarrow MB=MC\)
Vì \(\Delta ABM\)là tam giác đều có cạnh là 2cm\(\Rightarrow AB=AM=BM=2cm\)
Do đó độ dài cạnh BC là : \(2+2=4cm\)
Áp dụng định lý Py-ta-go trong tam giác vuông ABC ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AC=\sqrt{12}\left(cm\right)\)
b) Diện tích \(\Delta ABC\)là : \(\frac{1}{2}\left(AB.AC\right)=\frac{2.\sqrt{12}}{2}=\sqrt{12}\left(cm^2\right)\)