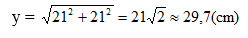Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


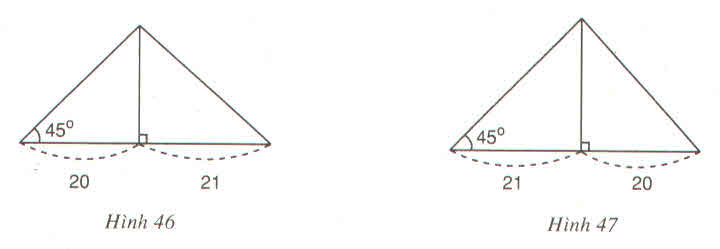
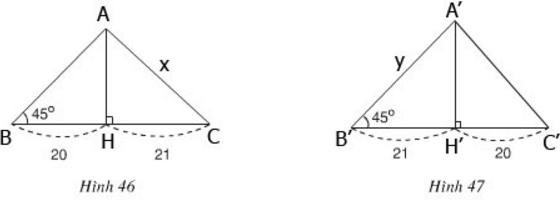
Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có:
Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có:

đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.

Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều