HP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 6 2017
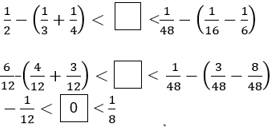
\(\dfrac{1}{2}-\left(\dfrac{1}{3}+\dfrac{1}{4}\right)< ...........< \dfrac{1}{48}-\left(\dfrac{1}{16}-\dfrac{1}{6}\right)\)
\(\dfrac{-1}{12}< .........< \dfrac{1}{8}\)và số ghi trong ô trống là số nguyên nên số đó phải là 0 .
NQ
1
14 tháng 1 2016
-2/3 và 3/4
-8/12......9/12
Vì -8<9 nên -8/12 < 9/12
Vậy: -2/3<3/4
VD
5
2 tháng 1 2016
Gọi trỗ trống là x , có:
-2/3 < x < 3/4 => -1 < x < 1
Vậy x = 0
27 tháng 5 2022
b: \(\left|x-\dfrac{3}{5}\right|< \dfrac{1}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{3}{5}>-\dfrac{1}{3}\\x-\dfrac{3}{5}< \dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\dfrac{4}{15}< x< \dfrac{14}{15}\)
c: \(\left|x+\dfrac{11}{2}\right|>-5.5\)
mà \(\left|x+\dfrac{11}{2}\right|\ge0\forall x\)
nên \(x\in R\)
1 tháng 6 2022
a: Gọi số nguyên cần tìm là x
Theo đề, ta có: \(\dfrac{1}{3}+\left(\dfrac{2}{4}-1\dfrac{2}{5}\right)< x< 2\dfrac{1}{7}+\left(\dfrac{-2}{5}-\dfrac{1}{4}\right)\)
\(\Leftrightarrow\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{7}{5}< x< \dfrac{15}{7}-\dfrac{2}{5}-\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20}{60}+\dfrac{30}{60}-\dfrac{84}{60}< x< \dfrac{15\cdot20-2\cdot28-35}{140}\)
\(\Leftrightarrow-\dfrac{34}{60}< x< \dfrac{209}{140}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)
b: Gọi số nguyên cần tìm là x
Theo đề, ta có: \(\dfrac{7}{3}+\dfrac{3}{4}-\dfrac{1}{5}>x>\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{2}{7}\)
\(\Leftrightarrow\dfrac{7\cdot20+3\cdot15-12}{60}>x>\dfrac{56-21+2\cdot12}{84}\)
\(\Leftrightarrow\dfrac{173}{60}>x>\dfrac{59}{84}\)
mà x là số nguên
nên \(x\in\left\{2;1\right\}\)
YY
0
18 tháng 6 2017
Ta có: \(\dfrac{a}{b}< \dfrac{c}{d}\Rightarrow ad< bc\)
\(\Rightarrow ad+cd< bc+dc\)
\(\Rightarrow d\left(a+c\right)< c\left(b+d\right)\)
\(\Rightarrow\dfrac{a+c}{b+d}< \dfrac{c}{d}\) (1)
\(ad< bc\)
\(\Rightarrow ad+ab< bc+ab\)
\(\Rightarrow a\left(b+d\right)< b\left(a+c\right)\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}\) (2)
Từ (1), (2) \(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\left(đpcm\right)\)
18 tháng 6 2017
Ta có :
\(\dfrac{a}{b}< \dfrac{c}{d}\Rightarrow ad< bc\)
\(\Rightarrow ad+ab< bc+ab\Rightarrow a\left(d+b\right)< b\left(c+a\right)\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}\left(1\right)\)
Lại có :
\(ad< bc\Rightarrow ad+cd< bc+cd\Rightarrow d\left(a+c\right)< c\left(b+d\right)\)
\(\Rightarrow\dfrac{a+c}{b+d}< \dfrac{c}{d}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\rightarrowđpcm\)
10 tháng 6 2017
|
Câu |
Đúng | Sai |
| a) Các số 7,5 và 12 là các ngọai tỉ | X | |
| b) Các số 4 và 7,5 là các trung tỉ | X | |
| c) Các số 4 và 22,5 là các trung tỉ | X | |
| d) Các số 22,5 và 12 là các trung tỉ | X | |
| e) Các số 7,5 và 22,5 là các ngoại tỉ | X |
TN
6 tháng 7 2017
| Câu | Đúng | Sai |
| a)Các số 7,5 và 12 là các ngoại tỉ | X | |
| b)Các số 4 và 7,5 là các trung tỉ | X | |
| c)Các số 4 và 22,5 là các trung tỉ | X | |
| d)Các số 22,5 và 12 là các trung tỉ | X | |
| e)Các số 7,5 và 22,5 là các ngoại tỉ | X |
\(\dfrac{1}{-5}>\dfrac{-3}{5}\)
\(\dfrac{1}{-5}=\dfrac{-1}{5}\)
\(=>\dfrac{-1}{5}>\dfrac{-3}{5}\)