Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Li độ dài ban đầu của nó là:
$x=\alpha.l=2$cm
Có: $\omega^2=\frac{g}{l}$
Áp dụng công thức liên hệ giữa li độ và vận tốc trong dao động điều hoà ta có:
$A^2=x^2+\frac{v^2}{\omega^2}$
$\Rightarrow A=2\sqrt2$cm

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

\(\overrightarrow {g'} =\overrightarrow g - \overrightarrow a \)
Ô tô chuyển động nằm ngang => \(\overrightarrow a \bot \overrightarrow g\)
=> \(g' = \sqrt{g^2+ a^2}\)
\(T = 2\pi \sqrt{\frac{l}{g}}\)
\(T' = 2\pi \sqrt{\frac{l}{g'}}\)
=> \(\frac{T}{T'} = \sqrt{\frac{g'}{g}} = \sqrt{\frac{\sqrt{g^2+a^2}}{g}} = 1,01\)
=> \(T'= \frac{2}{1,01} = 1,98 s.\)
cho mình hỏi: Nếu trong trường hợp ôtô chuyển động thẳng chậm dần đều thì phải làm ntn ?

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Ở VTCB lò xo dãn: \(\Delta \ell_0=10cm\)
Tần số góc: \(\omega=\sqrt{\dfrac{g}{\Delta\ell_0}}=10(rad/s)\)
Áp dụng công thức: \(v_0^2=v^2+\dfrac{a^2}{\omega^2}\)
\(\Rightarrow v_0^2=20^2+\dfrac{(200\sqrt 3)^2}{10^2}\)
\(\Rightarrow v_0=40(cm/s)\)
Biên độ dao động: \(A=\dfrac{v_0}{\omega}=4cm\)
Tỉ số giữa lực đàn hồi cực đại và cực tiểu:
\(\dfrac{F_{dhmax}}{F_{dhmin}}=\dfrac{k.(\Delta\ell_0+A)}{k.(\Delta\ell_0-A)}=\dfrac{\Delta\ell_0+A}{\Delta\ell_0-A}=\dfrac{10+4}{10-4}=\dfrac{7}{3}\)
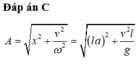
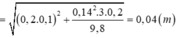

 =2 7,1 cm/s
=2 7,1 cm/s