Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do hứng được ảnh trên màn nên thấu kính đã sử dụng là thấu kính hội tụ.
b)
Đổi : \(AB=h=5\left(mm\right)=0,5\left(cm\right)\)
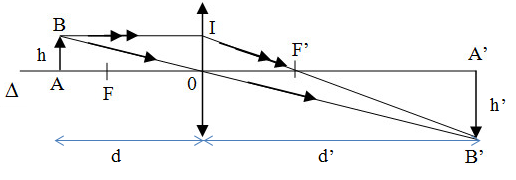
Xét \(\Delta OAB\sim\Delta OA'B'\) : \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\) (*)
Xét \(\Delta F'OI\sim\Delta F'A'B'\) : \(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\).
Mà \(OI=AB\) và \(F'A'=OA'-OF'\) nên \(\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\).
Từ đó, suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\Leftrightarrow\dfrac{18}{d'}=\dfrac{12}{d'-12}\Leftrightarrow d'=36\left(cm\right)\)
Thay lại vào (*) ta được : \(\dfrac{18}{36}=\dfrac{0,5}{h'}\Leftrightarrow h'=1\left(cm\right)\)
Vậy : Ảnh ở vị trí cách thấu kính 36cm và cao 1cm.

a, vì ảnh của vật AB là ảnh ảo
mà d>f (20cm>15cm) nên Thấu kính này là thấu kính phân kì
b,c, ta có 1/f=1/d'-1/d<=>1/15=1/d'-1/20<=>d'=60/7cm
có h/h'=d/d'<=>2/h'=20.7/60=>h'=6/7cm
Vậy vị trí của ảnh cánh thấu kính 1 khoảng = d'=60/7cm
độ cao của ảnh A'B'=6/7cm

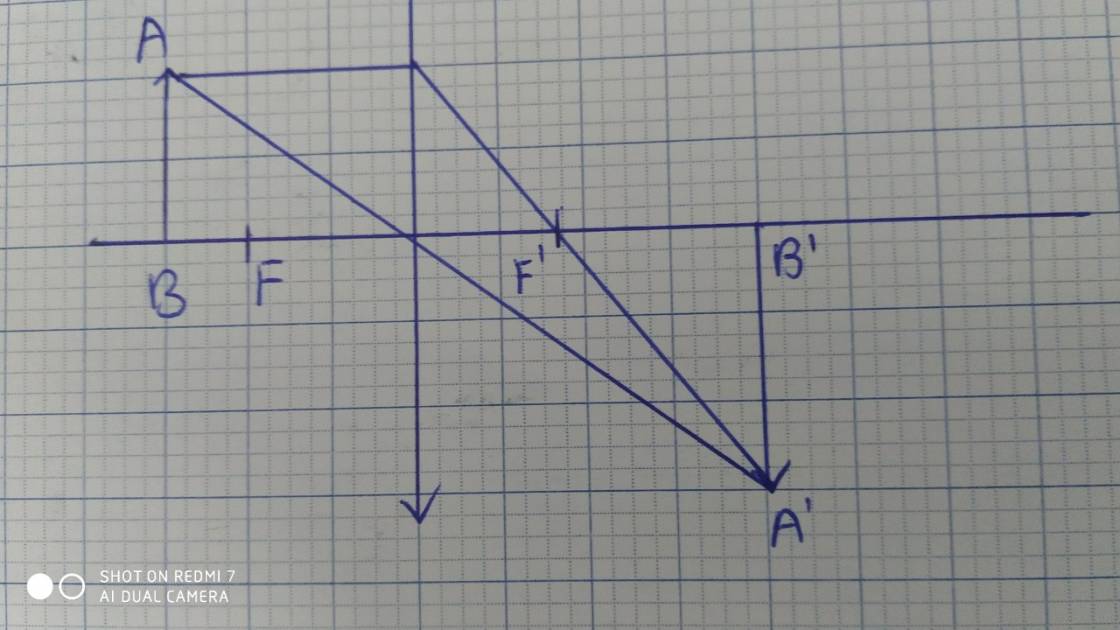
a)
b) Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow\dfrac{d}{h}=\dfrac{d'}{h'}\Leftrightarrow\dfrac{d'}{h'}=\dfrac{20}{2}\Rightarrow d'=10h'\)
Áp dụng công thức thấu kính ta được:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\left(1\right)\)
Thay \(d'=10h'\) vào công thức trên ta có:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{10h'}\) hay \(\dfrac{1}{12}=\dfrac{1}{20}+\dfrac{1}{10h'}\Rightarrow h'=3\left(cm\right)\)
Vậy chiều cao của ảnh là 3cm
Khoảng cách từ màn đến thấu kính:
Ta có: \(d'=10h'=10.3=30cm\)
gfvfvfvfvfvfvfv555