Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S là quãng đường ô tô đi đến chỗ bạn An.
\(S_1\) là khoảng cách từ nơi bạn An đứng đến nơi ô tô đang đứng.
\(S_2\) là khoảng cách từ chỗ bạn An đến đường quốc lộ.
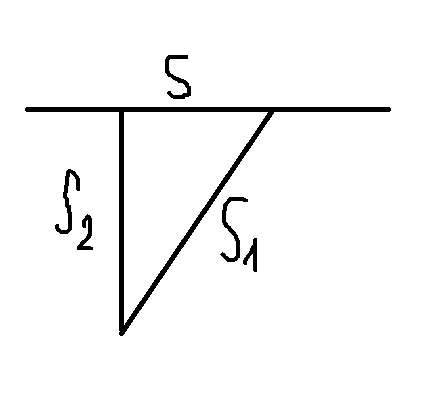
\(\Rightarrow S=\sqrt{S_1^2-S_2^2}=\sqrt{100^2-50^2}=50\sqrt{3}m\)
\(v=36\)km/h=10m/s
Thời gian ô tô đi đến chỗ bạn An:
\(t=\dfrac{S}{v}=\dfrac{50\sqrt{3}}{10}=5\sqrt{3}s\)
Vận tốc trung bình của An để vừa đón kịp xe:
\(v=\dfrac{S_1}{t}=\dfrac{100}{5\sqrt{3}}=\dfrac{20\sqrt{3}}{3}\approx11,55\)m/s

* Đề câu a hình như là tính v2 bạn nhé, vì v1 đề đã cho biết rồi
________________________________________
a) Thời gian đi của người anh là
\(t_1=\frac{S}{2v_1}+\frac{S}{2v_2}=\frac{S}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)\)
Mà vtb=8 km/h
=> \(\frac{S}{\frac{S}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{2v_1v_2}{v_1+v_2}=8\)
Thay v1=5
=> v2= 20
Mặt khác ta có
\(\frac{AC}{v_1}=\frac{BC}{v_2}=\frac{AC+BC}{5+20}=\frac{S}{25}\)=t' ( Trong đó C là điểm mà người em được bạn chở đi, còn AB là quãng đường từ nhà đến trường)
=> \(v_{tb}=\frac{S}{t'}=\frac{S}{\frac{S}{25}}=25\)( km/h)

Tốc độ trung bình của vật chuyển động trên cả đoạn đường AC là
\(v = \frac{S}{t} = \frac{AB+BC}{t_1+t_2} = \frac{v_1 t_1 + v_2 t_2}{t_1+t_2}.\)
câu trả lời của bạn Hai Yen sai rồi
phải tính từng vận tốc trung bình của vật đó ở trên từng qđ rồi mới tính vận tốc trung bình trên cả qđ

ta có:
thời gian người đó đi trên 1/3 đoạn đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{3v_1}=\frac{S}{180}\)
thời gian người đó đi quãng đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{2S}{3v_2}=\frac{2S}{270}\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{180}+\frac{2S}{270}}\)
\(\Leftrightarrow v_{tb}=\frac{S}{S\left(\frac{1}{180}+\frac{2}{270}\right)}=\frac{1}{\frac{1}{180}+\frac{2}{270}}\approx77\) km/h

Tóm tắt:
\(s=10m\)
\(v_2=3\)m/s
\(v=1m\)/s
\(v_1=5m\)/s
___________________________
Giải:
Thời gian chú chó chạy quãng đường dài 10m là:
\(t_1=\dfrac{s}{v_1}=\dfrac{10}{5}=2s\)
Quãng đường cậu bé đi được trong thời gian 2 giây là:
\(s_1=t_1.v=2.1=2m\)
Thời gian chú chó từ nhà đến lúc gặp cậu bé là:
\(t_2=\dfrac{s-s_1}{v_2+v}=\dfrac{10-2}{3+1}=\dfrac{8}{4}=2s\)
Quãng đường từ nhà đến vị trí chú chó gặp cậu bé là:
\(s_2=v_2.t_2=3.2=6m\)
Vận tốc trung bình là:
\(v_{tb}=\dfrac{s+s_2}{t_1+t_2}=\dfrac{10+6}{2+2}=\dfrac{16}{4}=4\)m/s
Vậy:...........................


Thời gian An chạy: \(t_1=\frac{AB}{v_2}=\frac{400}{0,6v_1}\)
Thời gian Bình chạy: \(t_2=\frac{AC}{v_1}+\frac{BC}{v_2}\)
Thay số ta chứng minh được t2<t1, Bình đến B trước An.
Đặt x = CD
\(t_1=\frac{AD}{v_2}=\frac{400}{0,6v_1}\)
\(t_2=\frac{AC}{v_1}+\frac{BC}{v_2}=\frac{320-x}{v_1}+\frac{\sqrt{x^2+240^2}}{v_2}=\frac{320}{v_1}+\frac{\sqrt{x^2+240^2}-0,6x}{0,6v_1}=\frac{320}{v_1}+\frac{y}{0,6v_1}\)
t1-t2>0
\(\Rightarrow t_1-t_2=\frac{400}{0,6v_1}-\frac{320}{v_1}-\frac{y}{0,6v_1}=\frac{400-192-y}{0,6v_1}>0\)
\(2018-y>0\Rightarrow0,64x^2-249,6x+14336< 0\Rightarrow70m< x< 320m\)
Hay \(0< AC< 250m\)
Khảo sát t2:\(t_2=\frac{320}{v_1}+\frac{y}{0,6v_1}\)
Để t2 cực tiểu thì y phải cực tiểu y= \(\sqrt{x^2+240^2}-0,6x\)
\(\Rightarrow0,64x^2-1,2xy+\left(240^2-y^2\right)=0\rightarrow\Delta\ge0\rightarrow y\ge192\)
Vậy \(y_{min}=192\Rightarrow x=-\frac{b}{2a}\)=180m. Khi đó AC=140m