
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\frac{1}{50}\) >\(\frac{1}{100}\)
\(\frac{1}{51}\)>\(\frac{1}{100}\)
\(\frac{1}{52}\)>\(\frac{1}{100}\)
..................
\(\frac{1}{99}\)>\(\frac{1}{100}\)
=>\(\frac{1}{50}\)+\(\frac{1}{51}\)+.............+\(\frac{1}{99}\)>\(\frac{1}{100}\).50=\(\frac{1}{2}\)(50 là số số hạng của S nha)
=>S>\(\frac{1}{2}\)

- Cạnh huyền góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì 2 tam giác đó bằng nhau.
- Cạnh góc vuông-góc nhọn kề: Nếu cạnh huyền và góc nhọn kề của tam giác vuông này bằng cạnh huyền và góc nhọn kề tương ứng của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Thêm một trường hợp khác nhé: cạnh huyền- cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và cạnh góc vuông tương ứng của tam giác vuông kia thì hai tam giác vông đó bằng nhau.
Học tốt
Định lí :
Trong tam giác vuông, mỗi cạnh góc vuông bằng :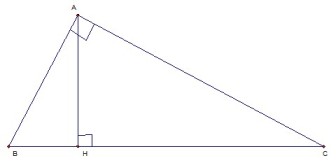
a) Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.
Công thức :
AC = BC.sin B = BC.cos C = AB.tg B = AB.cotg C.
AB = BC.sin C = BC.cos B = AC. Tam giác C = AC.cotg B

Đúng rồi ạ. Vẽ đối đỉnh là vẽ tia đối, x'A là tia đối của xA còn y'A là tia đối của yA

Câu a) thôi, câu b) chị chưa nghĩ được!
+) 2 số lẻ liên tiếp có dạng là 2n + 1 và 2n + 3 ( n thuộc N )
+) Đặt d thuộc ƯC ( 2n + 1; 2n + 3 ) ( d thuộc N* )
=> 2n + 1 chia hết cho d
2n + 3 chia hết cho d
Vậy ( 2n + 3 ) - ( 2n + 1 ) chia hết cho d
<=> 2 chia hết cho d
=> d thuộc Ư ( 2 )
=> d thuộc {1; 2}
Nhưng d là số lẻ => d ≠ 2 => d = 1
Vậy 2 số lẻ liên tiếp là 2 số nguyên tố cùng nhau.

Sử dụng Bất đẳng thức cô si:
Ta có: \(\frac{a}{b}+\frac{b}{a}\ge2\sqrt{\frac{a}{b}.\frac{b}{a}}\)
\(\Leftrightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Sử dụng hằng đẳng thức:
\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}=\frac{a^2-2ab+b^2}{ab}+2\)\(=\frac{\left(a-b\right)^2}{ab}+2\)
Vì \(\frac{\left(a-b\right)^2}{ab}\ge0\)\(\Rightarrow\frac{\left(a-b\right)^2}{ab}+2\ge2\)
Hay \(\frac{a}{b}+\frac{b}{a}\ge2\)
ta có: Ox là tia đối của Ox'
Oy là tia đối của Oy' (1)
ta có: góc xOy + góc xOy' = 180 độ ( kề bù)
góc xOy + góc x'Oy = 180 độ ( kề bù)
=> góc xOy + góc xOy' = góc xOy + góc x'Oy ( = 180 độ)
=> góc xOy' = góc x'Oy (2)
Từ (1);(2) => góc xOy' = góc x'Oy ( đối đỉnh)
x x' y' y o
p/s nha!