Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

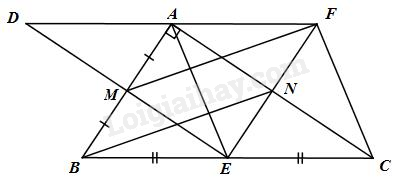
a) \(N\), \(E\) lần lượt là trung điểm của \(AC\) và \(BC(gt)\); Suy ra \(NE\) là đường trung bình của tam giác \(ABC\).
Suy ra \(NE\) // \(AB\)
Suy ra tứ giác \(ANEB\) là hình thang.
Mà \(\widehat {NAB} = 90^\circ \) (do \(\Delta ABC\) vuông tại \(A\))
Do đó tứ giác \(ANEB\) là hình thang vuông.
b) \(M\), \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME\) // \(AC\) hay \(ME\) // \(AN\)
Mà \(AM\) // \(NE\) (do \(AB\) // \(NE\))
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {{\rm{MAN}}} = 90^\circ \) nên \(AMEN\) là hình chữ nhật
c) Xét tứ giác \(BMFN\) có: \(MF\) // \(BN\) (gt) và \(BM\) // \(FN\) (do \(AB\) // \(NE\))
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (Tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\))
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD\) // \(BE\) hay \(AD\) // \(EC\)
Mà \(AF\) // \(EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE\) // \(AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\)(2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\)

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang

a) Xét \(\Delta\)ABC ta có :
M là trung điểm AB
N là trung điểm AC
=> MN là đường trung bình
=> MN//BC , MN = 1/2 BC (1)
=> MNCB là hình thang
b) Xét tam giác ABC ta có :
N , P là trung điểm AC , BC (2)
=> NP là đường trung bình
Từ (1) và (2) => MNPB là hình bình hành

a) Xét \(\Delta\)ABC có: M; N là trung điểm của AB; AC
=> MN là đường trung bình của \(\Delta\)ABC (1)
=> MN//BC
=> BCNM là hình thang
b) (1) => MN //= \(\frac{1}{2}\) BC mà BP = \(\frac{1}{2}\)BP va B; P; C thẳng hàng ( vì P là trung điểm BC )
=> MN// = BP => MNPB là hình bình hành
c) MN // BC => MN // HP => MNHP là hình thang
(b) => ^MNP = ^MBP => ^MNP = ^MBH (2)
Lại có: ^NMH = ^MHB ( so le trong ) ( 3)
Mặt khác: \(\Delta\)AHB vuông tại H có HM là trug tuyến đáy AB
=> HM = \(\frac{1}{2}\)AB = BM
=> \(\Delta\)MHB cân tại M => ^MBH = ^MHB (4)
Từ (2) ; (3) ; (4) => ^NMH = ^MNP
=> MNPH là hình thang cân
b) Điều kiện để HPNM là hình chữ nhật:
Ta có: HPNM là hình thang cân
=> HPNM là hình chữ nhật MH vuông góc BC
Mặt khác ta có: AH vuông góc BC
=> A; M; H thẳng hàng mà A; M; B thẳng hàng
=> H trùng B
=> Tam giác ABC vuong tại B.

Xét tam giác ABC có EA=EB ;MB=MC
suy ra ME là đường trung bình cũa tam giác ABC
suy ra ME // AC hay gócAEM=900 (1)
Tương tự góc MFA=900 (2)
góc EAF=900 (3)
từ (1) ;(2) ;(3) suy ra AEMF là hình chữ nhật

a)ta có : A=E=F=90 => AEHF hình chữ nhật
b)ta có: Am=AN, HM=MC =>ACNH hbh
Ta có AH//CN => AHE =CNH (đv) = FEH mà FC//NE => EFCN hìn thang cân
c)ta có OC, AM là trung tuyến của ∆ACH cắt nhau tại G => G là trọng tâm => AG =2/3 AM=2/3*AN/2=AN/3
=>AN=3AG
a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay BMNC là hình thang