Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A E C D Kẻ DE⊥ BC
Xét △ABC và △BDE có: Â=Ê=90*
∠ABD=∠DBE (BD phân giác ∠B)
BD: cạnh chung
⇒ △ABC = △BDE ( cạnh huyền-góc nhọn)
⇒ AD=DE ( 2 cạnh tương ứng)
Xét △EDC có: Ê=90*
⇒ Ê>∠C (theo nhận xét)
⇒ DC>DE (theo quan hệ góc,cạnh đối diện trong tam giác)
mà AD=DE ⇒DC>AD (đpcm)

Kẻ DH ⊥ BC.
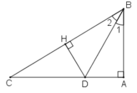
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC

A B C D
Xét hai tam giác vuông DBA và DHB có:
BD là cạnh chung
\(\widehat{ABD}=\widehat{DHB}\)( BD là tia phân giác )
\(\Rightarrow\Delta DBA=\Delta DBH\left(ch-gn\right)\)
\(\Rightarrow AB=DH\)( 2 cạnh bằng nhau )
Tam giác vuông DHC có:
DC là canh huyền suy ra DC là cạnh lớn nhất
\(\Rightarrow DC>DH\)
Mà DH = AD nên AD < DC
*Đảm bảo đúng 100% nhé!! 😊*
Giải:
Dựng DH vuông góc BC (H thuộc BC)
Xét hai tam giác vuông ABD và HBD có:
Góc A = Góc H (=90°)
BD: cạnh chung
Góc ABD = Góc HBD
=> Tam giác ABD = Tam giác HBD (cạnh huyền- góc nhọn)
=> AD = DH (2 cạnh tương ứng)
Xét tam giác vuông DHC vuông tại H có DC là cạnh huyền => DC là cạnh lớn nhất trong tam giác DHC
Do đó: AD = DH > DC (đpcm)

B1: Trên đoạn BC lấy điểm E sao cho E là chân đường cao lên điểm D.
Ta chứng minh tam giác ABD = tam giác EBD ( ch - gn)
=> AD = ED
Xét tam giác DEC vuông tại E có DC là cạnh huyền và DE là cạnh góc vuông
=> DC > DE
Mà DE = AD
Nên AD < DC (đpcm)

Câu B:
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC

Lời giải:
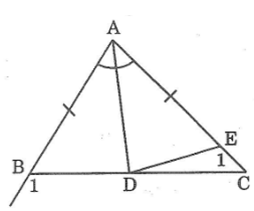
Trên cạnh AC lấy điểm E sao cho AE = AB.
Ta có: AB < AC nên AE < AC
Suy ra E nằm giữa A và C.
Xét ΔABD và ΔAED, ta có:
AB = AE (theo cách vẽ)
∠(BAD) = ∠(EAD) (gt)
AD cạnh chung
Suy ra: ΔABD = ΔAED (c.g.c)
Suy ra: BD = DE (2 cạnh tương ứng)
và ∠(ABD) = ∠(AED) (2 góc tương ứng)
Mà: ∠(ABD) + ∠B1= 180o (2 góc kề bù)
∠(AED) + ∠E1= 180o (2 góc kề bù)
Suy ra: ∠B1= ∠E1
Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B
Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)
Suy ra: ∠E1> ∠C
Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Vậy BD < DC.
Trên cạnh AC lấy điểm E sao cho AE = AB
AB < AC nên AE < AC => E nằm giữa A và C
Xét ∆ABD và ∆AED:
AB = AE (theo cách vẽ)
\(\widehat{BAD}=\widehat{EAD}\left(gt\right)\)
AD cạnh chung
Do đó: ∆ABD = ∆AED (c.g.c)
=> BD = DE (2 cạnh tương ứng)
\(\Rightarrow\widehat{ABD}=\widehat{AED}\)(2 góc tương ứng)
\(\widehat{ABD}+\widehat{B_1}=180^0\)(2 góc kề bù)
\(\widehat{AED}+\widehat{E1}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{B_1}=\widehat{E_1}\)
Trong ∆ABC ta có\(\widehat{B_1}\)là góc ngoài tại đỉnh B.
\(\Rightarrow\widehat{B_1}>\widehat{C}\)(tính chất góc ngoài tam giác)
\(\Rightarrow\widehat{E_1}>\widehat{C}\)
Trong ∆DEC ta có:\(\widehat{E_1}>\widehat{C}\)
=>DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Suy ra: BD < DC