Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

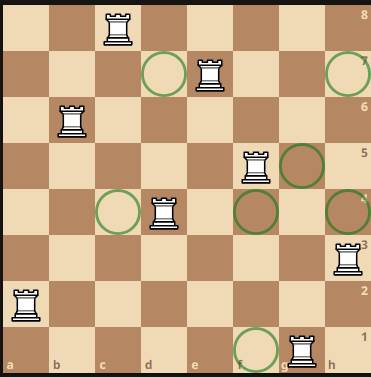
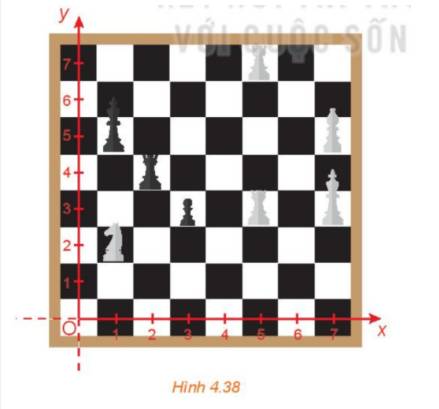
Vị trí của quân xe: hàng 3, cột c
Vị trí của quân mã: hàng 5, cột f

a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.

a) Việc xếp 9 viên bi sao cho không có hai viên bi trắng nào xếp liến nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh trước, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng vào 5 vị trí xung quanh bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5! = 120\) cách
Vậy có \(120.24 = 2880\) kết quả thuận lợi cho biến cố “Không có hai viên bi trắng nào xếp liền nhau”
b) Việc xếp 9 viên bi sao cho bốn viên bi xanh được xếp liền nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh liền nhau, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng có kích thước khác nhau vào bên trái hay bên phải của bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5!{.2^5} = 3840\) cách
Vậy có \(3840.24 = 92160\) kết quả thuận lợi cho biến cố “Bốn viên bi xanh được xếp liền nhau”

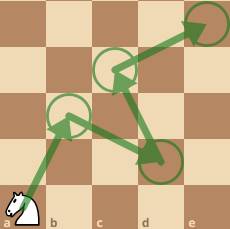
a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.
Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:
A có tọa độ (3; 3)
B có tọa độ (3; 1)
C có tọa độ (2; 0)
D có tọa độ (0; 0)
E có tọa độ (0; 4)
F có tọa độ (2; 4)
Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).




960 cách như tên
Cái mình cần là làm sao để tính ra được như vậy ấy.