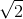Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pha của dòng điện so với điện áp là độ lệch pha của i đối với u mạch, nhưng nếu theo các phương án như đề bài thì mình nghĩ là tìm hệ số công suất của mạch.
Không mất tính tổng quát, ta lấy: \(U_R=3V\)
Suy ra: \(U_L=\sqrt{3}V\)
\(U_C=2\sqrt{3}V\)
\(\Rightarrow U=\sqrt{U_R^2+\left(U_L-U_C\right)^2}=2\sqrt{3}\)
Hệ số công suất: \(\cos\varphi=\frac{U_R}{U}=\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}\)

\(\leftrightarrow\frac{u^2_R}{\left(\frac{8}{5}\right)^2}+\frac{u^2_L}{\left(\frac{5}{2}\right)^2}=1\)
Điều kiện :
\(\begin{cases}u_R\le\frac{8}{5}\left(V\right)\\u_L\le\frac{5}{2}\left(V\right)\end{cases}\)
\(\Rightarrow U_{\text{oR}}=\frac{8}{5}\left(V\right);U_{0L}=\frac{5}{2}\left(V\right)\)
\(\Rightarrow\frac{R}{\omega L}=\frac{8}{5}.\frac{2}{5}=\frac{16}{25}\leftrightarrow L=\frac{25R}{16L}=\frac{1}{2\pi}\left(H\right)\)
Đáp án C

Điểu chỉnh điện dung C của tụ thấy C = C1 và C = C2 thì có cùng giá trị hiệu dụng của tụ điện \(U_{C1} = U_{C2}\).
Khi đó để \(U_{Cmax}\) thì \(C=C_0 = \frac{C_1+C_2}{2}\)
Chọn đáp án.D.

Bán kính của các hạt nhân chuyển động trong từ trường có biểu thức
\(R=\frac{mv}{qB}\)
=> \(R_{\alpha}=\frac{m_{\alpha}v_0}{q_{\alpha}B}=\frac{4.v_0}{2.q_e.B}=\frac{2v_0}{q_eB}.\left(1\right)\)
\(R_p=\frac{m_pv_0}{q_pB}=\frac{1.v_0}{q_e.B}=\frac{v_0}{q_eB}.\left(2\right)\)
\(R_T=\frac{m_Tv_0}{q_TB}=\frac{3.v_0}{q_e.B}=\frac{3v_0}{q_eB}.\left(3\right)\)
trong đó q là điện tích của hạt nhân = Z.q(e)
m là khối lượng hạt nhân = A(u)
Như vậy \(R_T>R_{\alpha}>R_T\)

Sử sụng hệ thức: 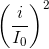 +
+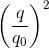 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 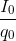 = 50 (rad/s)
= 50 (rad/s)